filmov
tv
Can You Solve A Cambridge Exam Question? Math Problem, 1802
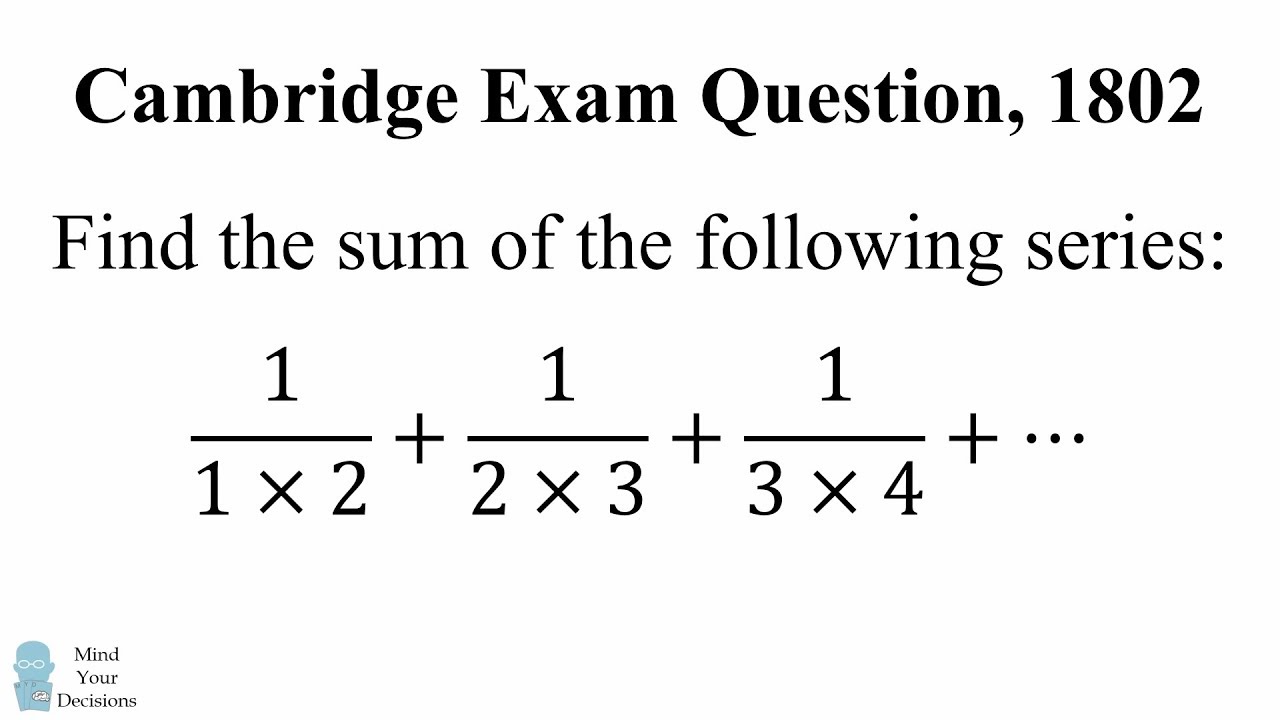
Показать описание
What is the sum of the series 1/(1×2) + 1/(2×3) + 1/(3×4) + ... ? This problem was part of the Cambridge Exam in 1802. Can you figure it out? Watch the video for a solution.
Thanks to all patrons! Special thanks to:
Marlon Forbes
Shrihari Puranik
Kyle
My blog post for this video:
Sources and resources
Cambridge problems. This problem is on page 22 of the document:
Check out Mathologer's video on Euler's series! It uses the series in this video to show the reciprocal sum of squares is bounded and therefore converges.
Connect on social media. I update each site when I have a new video or blog post, so you can follow me on whichever method is most convenient for you.
If you buy from the links below I may receive a commission for sales. This has no effect on the price for you.
My Books
"The Joy of Game Theory" shows how you can use math to out-think your competition. (rated 3.8/5 stars on 31 reviews)
"The Irrationality Illusion: How To Make Smart Decisions And Overcome Bias" is a handbook that explains the many ways we are biased about decision-making and offers techniques to make smart decisions. (rated 5/5 stars on 2 reviews)
"Math Puzzles Volume 1" features classic brain teasers and riddles with complete solutions for problems in counting, geometry, probability, and game theory. Volume 1 is rated 4.4/5 stars on 13 reviews.
"Math Puzzles Volume 2" is a sequel book with more great problems. (rated 5/5 stars on 3 reviews)
"Math Puzzles Volume 3" is the third in the series. (rated 3.8/5 stars on 4 reviews)
"40 Paradoxes in Logic, Probability, and Game Theory" contains thought-provoking and counter-intuitive results. (rated 4.3/5 stars on 12 reviews)
"The Best Mental Math Tricks" teaches how you can look like a math genius by solving problems in your head (rated 4.7/5 stars on 4 reviews)
"Multiply Numbers By Drawing Lines" This book is a reference guide for my video that has over 1 million views on a geometric method to multiply numbers. (rated 5/5 stars on 3 reviews)
Thanks to all patrons! Special thanks to:
Marlon Forbes
Shrihari Puranik
Kyle
My blog post for this video:
Sources and resources
Cambridge problems. This problem is on page 22 of the document:
Check out Mathologer's video on Euler's series! It uses the series in this video to show the reciprocal sum of squares is bounded and therefore converges.
Connect on social media. I update each site when I have a new video or blog post, so you can follow me on whichever method is most convenient for you.
If you buy from the links below I may receive a commission for sales. This has no effect on the price for you.
My Books
"The Joy of Game Theory" shows how you can use math to out-think your competition. (rated 3.8/5 stars on 31 reviews)
"The Irrationality Illusion: How To Make Smart Decisions And Overcome Bias" is a handbook that explains the many ways we are biased about decision-making and offers techniques to make smart decisions. (rated 5/5 stars on 2 reviews)
"Math Puzzles Volume 1" features classic brain teasers and riddles with complete solutions for problems in counting, geometry, probability, and game theory. Volume 1 is rated 4.4/5 stars on 13 reviews.
"Math Puzzles Volume 2" is a sequel book with more great problems. (rated 5/5 stars on 3 reviews)
"Math Puzzles Volume 3" is the third in the series. (rated 3.8/5 stars on 4 reviews)
"40 Paradoxes in Logic, Probability, and Game Theory" contains thought-provoking and counter-intuitive results. (rated 4.3/5 stars on 12 reviews)
"The Best Mental Math Tricks" teaches how you can look like a math genius by solving problems in your head (rated 4.7/5 stars on 4 reviews)
"Multiply Numbers By Drawing Lines" This book is a reference guide for my video that has over 1 million views on a geometric method to multiply numbers. (rated 5/5 stars on 3 reviews)
Комментарии
 0:24:48
0:24:48
 0:04:27
0:04:27
 0:03:55
0:03:55
 0:12:33
0:12:33
 0:05:33
0:05:33
 0:10:22
0:10:22
 0:11:45
0:11:45
 0:11:15
0:11:15
 0:48:15
0:48:15
 0:01:20
0:01:20
 0:05:41
0:05:41
 0:00:57
0:00:57
 0:08:19
0:08:19
 0:10:15
0:10:15
 0:06:34
0:06:34
 0:05:45
0:05:45
 0:04:55
0:04:55
 0:06:41
0:06:41
 0:03:05
0:03:05
 0:08:03
0:08:03
 0:09:25
0:09:25
 0:01:35
0:01:35
 0:11:27
0:11:27
 0:04:02
0:04:02