filmov
tv
Cambridge Test | Can You Solve?
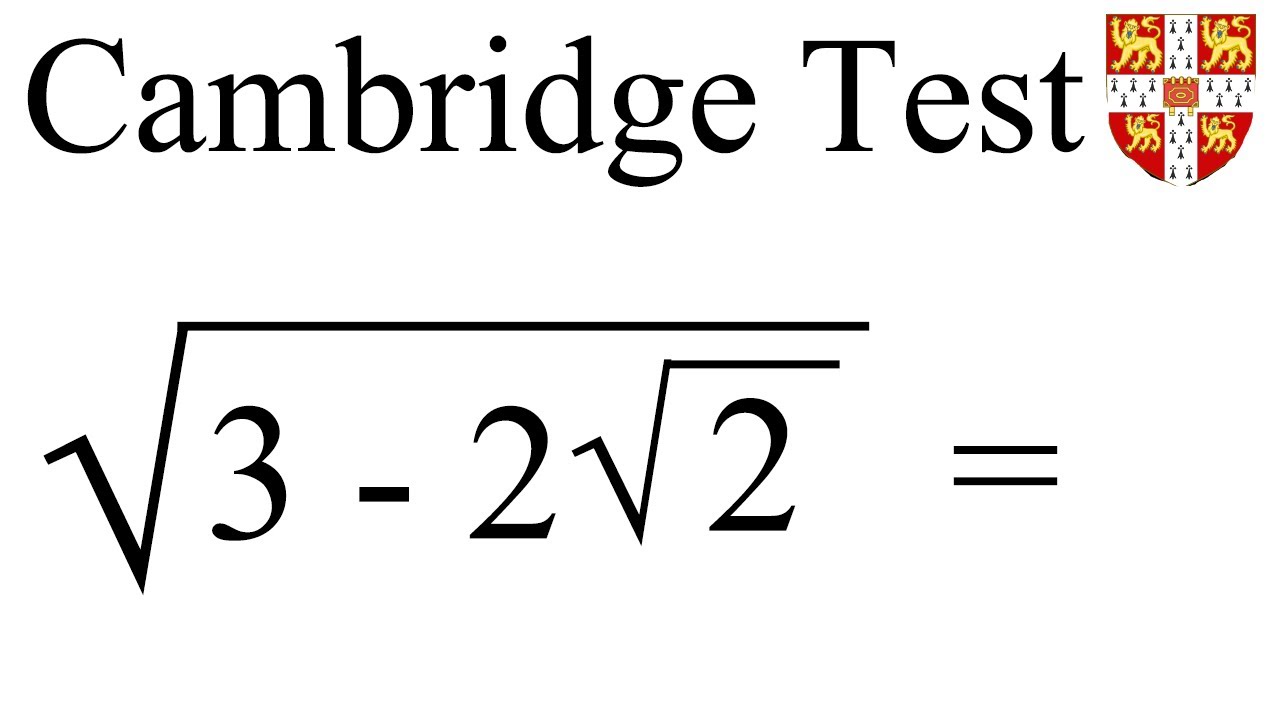
Показать описание
Hello. In this video, i am going to show you a great Algebra question that you can use to practice your math skills. This question is sure to challenge your algebra knowledge, so make sure you practice this trick today! With practice, you'll be able to tackle any algebra problem with ease!
On this channel, you will get best math problems, questions and solutions to improve your math skills. Subscribe to my YouTube channel. Thank you and have a good day:))
Thank you:)
#maths #algebra #mathematics #mathematician #mathematicians #algebra #algebratricks #algebraformulas #algebrahelp #olimpiadas #olimpiadmath #algebraquestion #algebraquestions #geometry #easymaths #easymathematics #easymathematicsforyou #multiplication #division #fraction #product #laws #lawsofexponent #howtolearnmathsfromthebeginning #howtolearnmathsfrombasics #howtolearnmaths #simplemathstricks #simplemathematics #simplemath #algebrahelp #simplealgebra#relaxingmath#howtosolvepotentialequations#potentialequations#solveforx#mathssolving#exponents #equations #exponentialequation #exponentialequations #algebrahelp #algebraformulas #algebratrick #highermathematics #highermaths #highermath#programming #programmer#sinus#sinx#cosx#findthevalueof
#powerdivision#olympiadalgebra#olympiadclass8
On this channel, you will get best math problems, questions and solutions to improve your math skills. Subscribe to my YouTube channel. Thank you and have a good day:))
Thank you:)
#maths #algebra #mathematics #mathematician #mathematicians #algebra #algebratricks #algebraformulas #algebrahelp #olimpiadas #olimpiadmath #algebraquestion #algebraquestions #geometry #easymaths #easymathematics #easymathematicsforyou #multiplication #division #fraction #product #laws #lawsofexponent #howtolearnmathsfromthebeginning #howtolearnmathsfrombasics #howtolearnmaths #simplemathstricks #simplemathematics #simplemath #algebrahelp #simplealgebra#relaxingmath#howtosolvepotentialequations#potentialequations#solveforx#mathssolving#exponents #equations #exponentialequation #exponentialequations #algebrahelp #algebraformulas #algebratrick #highermathematics #highermaths #highermath#programming #programmer#sinus#sinx#cosx#findthevalueof
#powerdivision#olympiadalgebra#olympiadclass8
Комментарии
 0:06:37
0:06:37
 0:07:19
0:07:19
 0:03:55
0:03:55
 0:20:26
0:20:26
 0:06:49
0:06:49
 0:07:42
0:07:42
 0:05:50
0:05:50
 0:04:04
0:04:04
 0:08:10
0:08:10
 0:04:15
0:04:15
 0:10:32
0:10:32
 0:09:04
0:09:04
 0:15:13
0:15:13
 0:05:51
0:05:51
 0:00:59
0:00:59
 0:14:23
0:14:23
 0:07:08
0:07:08
 0:17:50
0:17:50
 0:09:05
0:09:05
 0:10:48
0:10:48
 0:09:08
0:09:08
 0:13:08
0:13:08
 0:00:44
0:00:44
 0:07:31
0:07:31