filmov
tv
Can you solve this Cambridge Interview Question? Simplify the Radical | No Calculators Allowed!
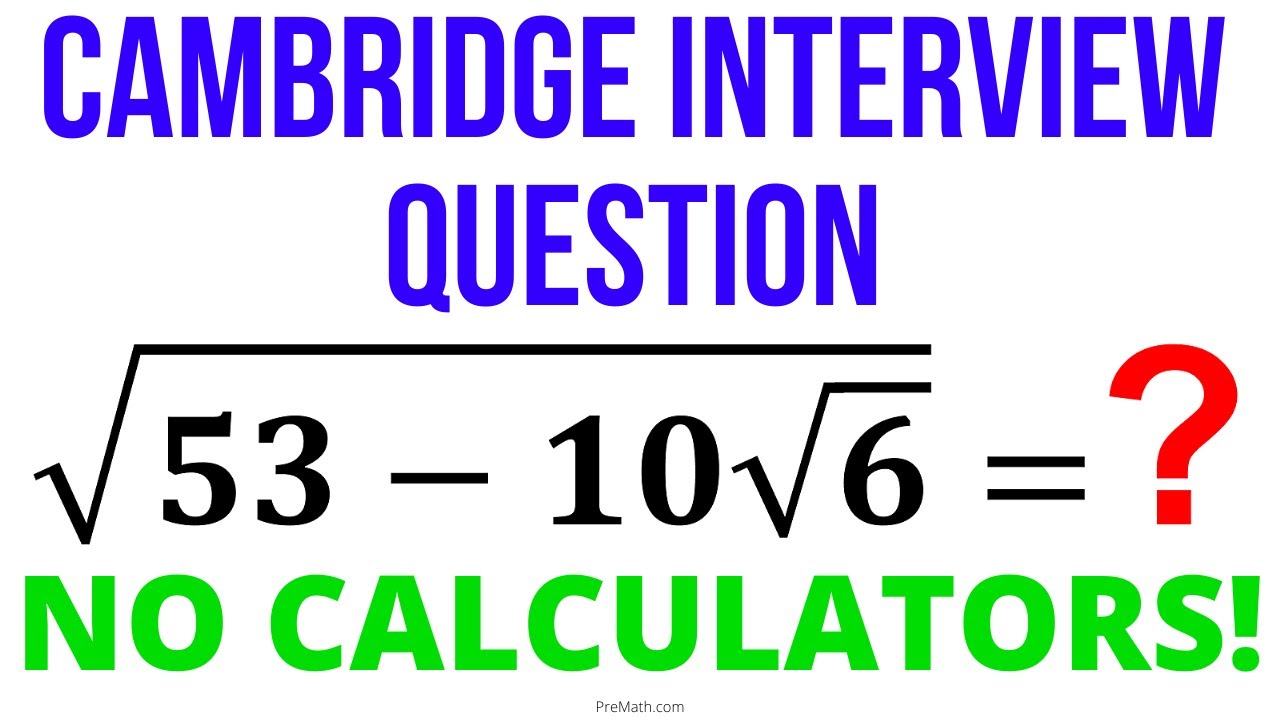
Показать описание
Can you solve this Cambridge Entrance Exam Question?
Can you solve this Cambridge Entrance Exam Question?
Cambridge Test | Can You Solve?
Can You Pass Cambridge Entrance Exam?
Can You SOLVE This Cambridge Entrance Exam | OLYMPIAD MATH
Cambridge interview problems can you solve this | Cambridge interview Question #cambridge
Can you solve this Cambridge Interview Question? Two Methods! | Fast & Easy Explanation
Cambridge Interview Question! Can you solve this problem? | Step-by-Step Tutorial
A very tricky Cambridge University Admission Algebra Exam | Entrance Aptitude Test | Find C!!
Can YOU Solve This Cambridge Interview Question? #Shorts #Cambridge #math
Cambridge University test | Can you solve this?
Can you solve this Cambridge Entrance Exam Question? | A nice Math Olympiad Problem.
Cambridge Test | Can You Solve?
Cambridge Exam | Can You Solve This Algebra Question?
A very tricky Cambridge University Admission Algebra Exam | Entrance Aptitude Test | Find x!!
Can you Solve this Cambridge Interview Question?
Can you Solve Cambridge University Admission Test ?✍️🖋️📘💙
Can you solve this Cambridge Exam Question?
Can you Solve Cambridge University Admission Test ?✍️🖋📘💙 #maths #education #squareroot #math...
Can you Pass Cambridge University Entrance Test? ✍️🖋📘💙 #maths #education #exponents
Cambridge English - How To Pass Listening
Can you Solve Cambridge University Admission Test ?✍️🖋️📘💙
Can You Solve Cambridge University Entrance Interview Question? How To Solve!!!
Can You Solve This Cambridge Exam Question? | Number Theory | Infinite Descent
Комментарии
 0:12:42
0:12:42
 0:24:48
0:24:48
 0:03:55
0:03:55
 0:10:32
0:10:32
 0:03:42
0:03:42
 0:04:27
0:04:27
 0:11:56
0:11:56
 0:09:25
0:09:25
 0:09:49
0:09:49
 0:00:57
0:00:57
 0:10:05
0:10:05
 0:20:45
0:20:45
 0:10:22
0:10:22
 0:11:45
0:11:45
 0:09:15
0:09:15
 0:12:33
0:12:33
 0:09:16
0:09:16
 0:08:28
0:08:28
 0:06:44
0:06:44
 0:06:02
0:06:02
 0:14:03
0:14:03
 0:08:37
0:08:37
 0:12:49
0:12:49
 0:03:05
0:03:05