filmov
tv
A Nice Exponential Equation. Solve x^x=2^2048.

Показать описание
Simple exponential equation. Solve for x.
घातीय समीकरणों को कैसे हल करें.
如何求解指数方程。
如何求解指數方程。
Cómo resolver ecuaciones exponenciales.
Math Olympiad Trick
Math Olympiad Question
गणित ओलंपियाड ट्रिक
奥林匹克数学技巧
奧林匹克數學技巧
truco de la olimpiada de matemáticas
घातीय समीकरणों को कैसे हल करें.
如何求解指数方程。
如何求解指數方程。
Cómo resolver ecuaciones exponenciales.
Math Olympiad Trick
Math Olympiad Question
गणित ओलंपियाड ट्रिक
奥林匹克数学技巧
奧林匹克數學技巧
truco de la olimpiada de matemáticas
A Very Nice Exponential Equation | Can you solve?
X=? A Nice Exponential Equation #maths #shorts #exponentialequation #matholympiad
A Nice Exponential Equation
Solving A Nice Exponential Equation
Solving a Nice Exponential Equation in Two Ways
Solving A Nice Exponential Equation
A Nice Exponential Equation
A Nice Exponential Equation | Math Olympiads
A nice exponential equation ।। solve for x @mathscuriosity494 #mathsolympiad #exponentialequation...
Solving A Nice Exponential Equation | Real and Complex
A Nice Math Olympiad Exponential Equation 3^x = X^9
A Nice Exponential Equation solving. Learn This Maths Tricks @rashel1
A Nice Exponential Equation | Can you solve?
A Nice Exponential Equation #algebra
Solving A Nice Exponential System
A Nice Exponential Equation
A Nice Exponential Equation | Math Olympiads
Math Olympiad Question A Nice Exponential Equation
A Nice Exponential Equation
A Nice Olympiad Exponential Multiplication Problem #short #olympiad #mathematics #maths #exponents
Solving Exponential Equation
A Nice Exponential Equation (5^x-3^x=16)
A Nice exponential equation problem. #matholympiadproblem #mathshorts #exponential
🔥 Solving A Nice Exponential Equation 6^x=60 | A Nice Math Olympiad Exponential Equation
Комментарии
 0:09:21
0:09:21
 0:01:01
0:01:01
 0:00:48
0:00:48
 0:06:30
0:06:30
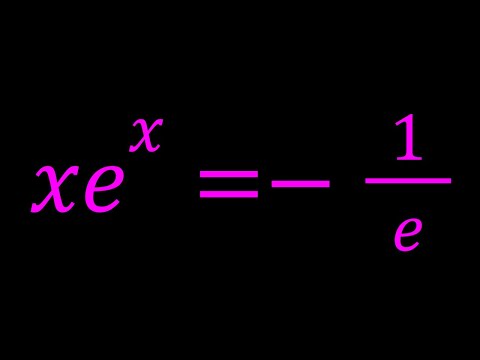 0:11:14
0:11:14
 0:09:56
0:09:56
 0:08:50
0:08:50
 0:06:50
0:06:50
 0:05:36
0:05:36
 0:10:28
0:10:28
 0:02:34
0:02:34
 0:03:33
0:03:33
 0:08:46
0:08:46
 0:07:36
0:07:36
 0:09:00
0:09:00
 0:01:00
0:01:00
 0:08:21
0:08:21
 0:00:22
0:00:22
 0:00:31
0:00:31
 0:00:52
0:00:52
 0:00:54
0:00:54
 0:06:37
0:06:37
 0:00:26
0:00:26
 0:05:42
0:05:42