Geometric Algebra in 2D - Fundamentals and Another Look at Complex Numbers

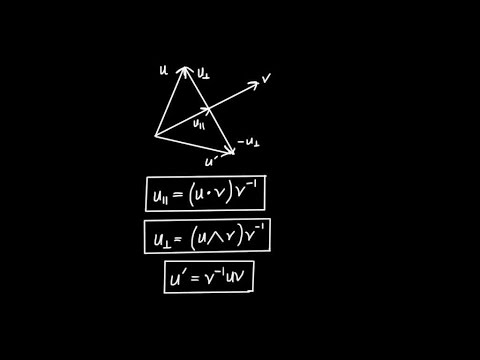
In this video, I introduce some of the concepts of geometric (Clifford) algebra, focusing on two-dimensional space (R^2). We'll talk about the wedge (exterior) product, review the dot product, and introduce the geometric product. We'll see that a new mathematical object, the bivector, arises from considering the wedge product. Furthermore, we're going to see that this bivector behaves like an imaginary unit in that it squares to -1. Since it has this property, it naturally relates to vector rotation in 2D, like the complex numbers.

Recommended video on Clifford algebra:

[rsanden]

Awesome series. Every step flows from the previous one in a logical and seamless manner such that the viewer never becomes lost trying to connect missing dots along the way. The fact that your train of thought transports its passengers to the final destination instead of casting them aside is the greatest praise I could bestow on any teacher. Well done!

[processing]

I recently saw a blog post about Clifford Algebra and how beautiful it is. Ever since, I've been trying to learn more, but couldn't find a gentle introduction to the topic that still goes deep into the math. Thank you for these great videos--they do exactly that. You are a gifted teacher.

[reasonablefellow]

Thanks for publishing this series, it's led me down the Geometric Algebra rabbit hole.

Geometric Algebra does away with ideas in mathematics I find aesthetically unpleasing (e.g. cross products, determinants, unmotivated definition of i=sqrt(-1), superfluous coordinate systems) and replaces them with something more unified, beautiful, and intuitive.

I don't understand why the subject is not more popular. My impression from googling is that the subject has been stagnant for the past decade. Books on the subject are mostly aimed at higher-level physics students. Why has no one written an introductory Physics book using Geometric Algebra? If I learned this stuff in high school or early college, I would have been a better student.

Also from googling, my impression is that amateur mathematicians/physicists get more excited about the subject than the experts do. Is Geometric Algebra not as attractive as it appears on the surface, or do amateurs just appreciate good pedagogy more than most experts do?

[MultivectorAnalysis]

At 11:24 you mentioned that it was Clifford who came up with the geometric product of vectors as the sum of Grassmann's inner and outer (dot and wedge) products. That's what many GA practitioners think, and it is correct, but I found it fascinating to learn that Grassmann independently came up with that idea near the end of his life. In the paper "Grassmann's Vision, " Hestenes points out that Grassmann (influenced by Hamilton's quaternions) defined what he called the "central product" in a paper that was actually published before Clifford's paper introducing the geometric product. Fascinating stuff!

[pi]

"I could cook up some vector, 'v.'"

*inhales deeply*

Smells good

[makespace]

Totally agree with @Ryan Sanden. No missing, unexplained or jumped steps. Pace is perfect. Best math instructional vid series that I've seen.

[movingheadmau]

Read a recommendation to this series in a comment under another video, and I must say, this is very well explained. Thank you for sharing this video-series with us!

[sramanabiswas]

I am a Phd (physics) scholar from India and I want to say thank you from core of my heart. Great series indeed!!!👍

[spicemasterii]

I've been waiting for your video on geometric algebra. Finally! Thank you for an awesome introduction. Very clearly explained. Looking forward to more on this topic. Thanks again!

[omkark]

Perfect example of video... Nicely explained. Thank you.

[JobvanderZwan]

These videos are really great; I haven't binged on a mathematics playlist like this since first discovering 3blue1brown!

As a physics dropout who got super-frustrated with the lack of an intuitive feeling for what the mathematics I was taught was doing (aside from, you know, just sucking at it), this feels like such a simple and intuitive foundation connecting a whole lot of not-quite-as-intuitive mathematics together.

I'm starting to wonder if it wouldn't make much more sense to introduce GA immediately after introducing vectors in high school, even before complex numbers. You know, when vectors are just arrows that you can add and subtract, representing Newtonian forces.

[anthonysegers]

This video is so much more than it's title implies. It opens the door to Geometric Algebra, Cartan's Exterior Algebra, Modern Physics and a way of thinking about deep and beautiful correspondences and analogies.

[thoughtupquick]

the way these random algebras map to real things, feels mystical, like it was the reason people chased it for so long.

[markwarren]

Many thanks for this exhaustive focus on just 2D demonstrating the isomorphism of Geometric product to the complex number. Revealed crucial new connections that help understanding of the Clifford/Geometric Algebra .

[blackedoutk]

Amazing video! I got especially excited upon seeing cos(theta) + sin(theta)*I, because that reminded me of quaternions. Hyped to watch through the rest of this series, thanks for creating it

[bobkelly]

A model of clarity my man! You have a new sub.

[MrRyanroberson]

29:50 if you instead view a vector (ae1+be2) as being e1(a+be1e2), then it makes sense why left and right multiplication by e1e2 is different. in fact, the e1 factor can be thought of as a "mapping" from the true complex numbers (a+be1e2) to the vectors (ae1+be2) for the purposes of graphing

[freddavis]

Your videos on Geometric Algebra really are great. Thanks a lot for making them :)

[IznbranahlGoose]

Thanks for this series. A few days ago I was trying to find more
information on quaternians and rotating objects in higher dimensions and then *poof* your video introducing rotors came out... but first I had to find out what geometric algebra was all about.

[defnotadrian]

Thank you so much for these videos on Geometric Algebra they have cleared up a lot of doubts I've had in it.