filmov
tv
Finding the Area of Arbitrary Polygons With Geometric Algebra

Показать описание
In this short, I show a method that can be used to find the area of any polygon using geometric algebra.
Patreon Supporters:
Christoph Kovacs
David Johnston
Jason Killian
LoganMP
Richard Penner
Rosario
Patreon Supporters:
Christoph Kovacs
David Johnston
Jason Killian
LoganMP
Richard Penner
Rosario
Finding the Area of Arbitrary Polygons With Geometric Algebra
How to find the areas of irregular shapes (including Pick's formula)
Python Calculate the area between arbitrary points
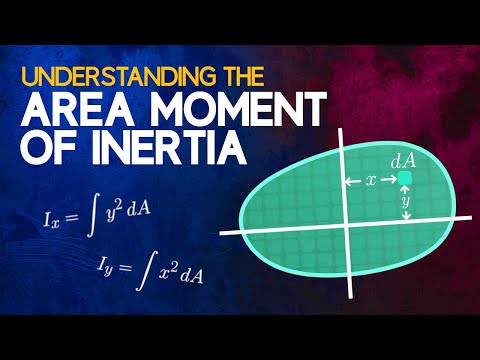
Understanding the Area Moment of Inertia
Area of Arbitrary Triangle
How to find height and understand the formula for area of an oblique triangle
Day 9 HW (4) Finding the Area of a Polygon Using Matrices
14.05.04 Surface Area for an Arbitrary Surface
Magnificent Mountains 1- Where do we find mountains?
Calculus5g Finding area under a curve manually with paper and scissors.
Calculus 1 Lecture 4.3: Area Under a Curve, Limit Approach, Riemann Sums
Surface Area of a Sphere (equation derived with calculus)
Area under Excel plot | Method explained
Area Challenge: Find the Area of a Polygon With Sides of Missing Length
Engineering: Determine surface area of arbitrary physical object (3 Solutions!!)
Triangle area proofs | Perimeter, area, and volume | Geometry | Khan Academy
Find the area under sec^2x
What Is the Area of a Regular Hexagon With a 4-inch Side?
Calculus 2: Area of a Surface of Revolution (Video #9) | Math with Professor V
Volume of solids of revolution about lines other than x or y axis
Calculus - Area under Simple Curves | Don't Memorise
Math 31 Area Under a Curve Lesson
Area of a Polygon using matrices
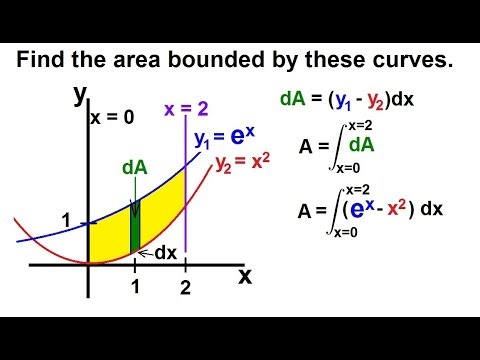
Calculus 2 - Integration: Finding the Area Between Curves (1 of 22) Ex. 1: y=e^x, y=x^2, x=0, x=2
Комментарии
 0:00:52
0:00:52
 0:09:22
0:09:22
 0:02:16
0:02:16
 0:11:05
0:11:05
 0:05:58
0:05:58
 0:07:38
0:07:38
 0:17:59
0:17:59
 0:08:47
0:08:47
 0:36:27
0:36:27
 0:10:57
0:10:57
 2:07:03
2:07:03
 0:05:14
0:05:14
 0:04:32
0:04:32
 0:01:00
0:01:00
 0:02:17
0:02:17
 0:10:23
0:10:23
 0:04:05
0:04:05
 0:03:00
0:03:00
 0:29:32
0:29:32
 0:18:32
0:18:32
 0:03:10
0:03:10
 0:30:12
0:30:12
 0:04:05
0:04:05
 0:06:13
0:06:13