Quaternions Are Not Four-Dimensional Objects

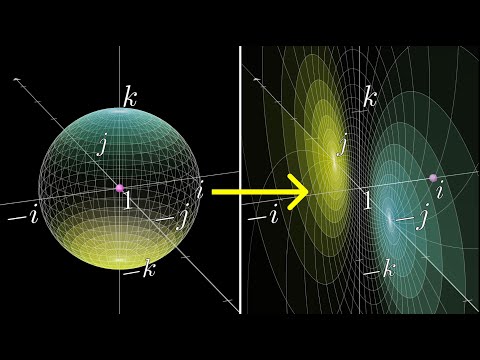
In this short, I argue that quaternions are three-dimensional objects, not four-dimensional objects, because of how quaternions arise naturally in three-dimensional geometry. Check out my channel for more on geometric algebra.

Patreon Supporters:
Christoph Kovacs
David Johnston
Jason Killian
LoganMP
Richard Penner
Rosario

[flamewingsonic]

I want to quibble a bit. You are confusing the dimension of an object with the dimension of the vector space at the center of the geometric algebra.

Quaternions *are* 4D: they reside in a 4D subalgebra of the full 3D geometric algebra, which has 8 dimensions. I will agree that a pure imaginary quaternion (to use the "standard" terminology; i.e., no scalar part) is a 3D object because it resides in the 3D subalgebra of bivectors. But a full quaternion cannot be correctly represented in 3D (or in the 3D subalgebra of bivectors) because it requires discarding information (the scalar part) to do so.

You are also confusing the dimension of a single specific parabola with the dimension of all possible parabolas; given there are 3 parameters in the expression of a parabola, any specific set will, indeed, be a 2D object; but the space of all parabolas (obtained by considering all possible values of the parameters) is 3D, even though every specific parabola is 2D.

[jeffbarrett]

Could one say that quaternions are four dimensional, and UNIT quaternions are three dimensional? (4 for the quaternions - 1 constraint)

[mikip]

I think this is just semantics. A parabola can indeed be conceptualized as a vector in 3D parameter space.

[Qhartb]

Man, this post made me angry and I'm frustrated that it's actually driving me to engage and give indicators to the algorithm but...

Quaternions are unambiguously 4D objects. I think your point is that they are objects that can naturally arise in 3D geometry, but that's not the same thing. Real scalars are also natural objects in 3D geometry, but we don't say that they're 3D objects -- they're obviously 1D.

[sudgylacmoe]

I feel like a lot of people have been misunderstanding the point of this video, so I thought I would clarify several things.

Yes, I know that algebraically, quaternions are four-dimensional in the sense of the usual definition of dimension given in linear algebra. I am not disputing this fact. That's why I said "While they do have four components" in the video. I was trying to (unsuccessfully apparently) stop people from making this particular objection.

One underlying point that most people didn't get is that I'm trying to distinguish between algebraic dimension and geometric dimension. I will admit that I don't have a fully rigorous definition of geometric dimension, but the point of this video is not to be rigorous. My main reason for making this was seing people try to give "intuitive" descriptions of quaternions using four-dimensional geometry, and I was trying to provide a counterpoint to those descriptions. I do believe that fundamentally, quaternions live in 3D geometric space, not 4D, so these descriptions have always bothered me.

I do want to point out that yes, there are several issues with the comparison with parabolas. The reason I put that in there was to show that there is a distinction between algebraic and geometric dimension, even though the details of this particular example are not good. I have better examples in this regard (particularly from projective geometry as another commenter pointed out), but I picked this one because I felt like the accessibility of using an object we all learn in high school outweighed the issues the example had.

I know some people might still argue that you can still use quaternions in 4D geometry, so we shouldn't say that they are not 4D geometric objects. Now I disagree with the conclusion in that argument, because I think that using 3D GA is the most natural way to derive quaternions, so they are more 3D than 4D. But at this level I do recognize that this is a bit more subjective. Which is great! This is the kind of topic we can have an actual discussion on! But the rest of the comments on this video are missing the point of the video (which I will admit is partially my fault).

Edit: Another argument I see people saying is "quaternions being able to represent 3D rotations does not necessarily make them 3D!" I actually agree with that argument. My point in bringing up 3D rotations in the video was not to say that this is why quaternions are 3D objects, but just to show one of the many things that quaternions do as 3D objects. The reason that quaternions are 3D objects is that they are the combination of a scalar and a 3D plane. Because 3D planes are 3D, quaternions are 3D too. (While scalars are 1D algebraically, they don't really have a dimension geometrically so they don't affect the overall geometric dimension of the object.) The fact that they represent 3D rotations is just a bonus. Oh and also, the argument "the only quaternions that represent 3D rotations are the unit quaternions so you're not including all quaternions" is flawed. All quaternions, normalized or not, represent 3D rotations in the same way as long as you use the inverse instead of the conjugate.

[dmr]

This is misleading, verging on incorrect. It’s true that isomorphism classes of quaternion rings over R correspond bijectively to the orbits of the group GL3(R) which has dimension 3 over R, but the far more important property they possess (in terms of dimension theory at least) is that the n-dimensional quaternionic space is a 4n-dimensional vector space over the real numbers. If you take the ring of real Hamilton quaternions, the Krull dimension is 4. The complex numbers are a degree-2 field extension over the real numbers, and the Cayley–Dickson construction that produces the quaternions from the complex numbers is the same as that which yields the complex numbers from the reals, implying at least heuristically that the quaternions ought to be considered as 4-dimensional. Just because the quaternions act on 3 dimensional space does not in any way mean that the objects themselves are 3-dimensional.

[davidgillies]

I think the main upshot of this short is that when you use the word dimension, define your context. *Unit* quaternions are isomorphic to SU(2), which is three dimensional, and diffeomorphic to the 3-sphere, also three dimensional. It's unit quaternions that we use to represent 3D rotations. But general quaternions can be identified naturally with R^4 or C^2, and those most certainly are four dimensional.

[evandrofilipe]

# The problem
To my understanding of this, it seems people are mixing up algebraic dimension and geometric dimension.

# What is dimension?
Algebraic dimension means how many parameters are there (obviously of objects that don't collect).
Geometric dimension to *my* knowledge is how many basis vectors the thing we are describing has.

# Dimension conclusion
So algebraicly, a + bi + cj + dk has 4 params (a, b, c and d). Geometrically, i, j and k are bivectors made of 3 basis vectors (e1, e2, e3). The scalar can be formed of these basis vectors therefore it doesn't need another basis vector to describe.

# Well, which one is better?
Whether one or another is more useful is seemingly undecided for a lot of people.

# Personally
Personally, since we are talking about rotations, I find it easier to think about in terms of what makes up the objects attatched to the parameters that have a unique effect on the resulting thing (idk what to call it).
I think the phrase "degrees of freedom" can be misleading when talking about *geometric* algebra where what we care about is the effect something has. For example, I could not tell you at a glance what the scalar part does to the rotation in question except that it has something to do with scaling. But in the ga version I know it will have no effect on the angle and I can safely ignore it. Now that example may be schizo ramblings but I just think that ga is generally easier to reason about.

[AlfredDiffer]

Heh. My advisor used to make this point too. Problem is people are VERY hooked on the idea that 'dimension' means the number of elements in the spanning set of the vector space. Your algebraic dimension. My advisor had to work hard to get us to admit the possibility that 'dimension' might mean something else.

I settled on something that still looks like the size of a spanning set, but where we are allowed to use another operation. (scaling, adding, & multiplying)

[gavintillman]

I’d agree that unit quaternions are 3d. Pick an axis (2d) and angle (1d) and you can represent in 3d. But non unit quaternions also have a scaling which is your 4th dimension.

[caspermadlener]

The projective plane consists of the different different ratios (x:y:z).
Even though you require three variables to properly represent the projective plane, it inhibits intersection behaviour like it has two dimensions.

I feel like quaternion rotation is similar. They have four components, but a lot of quaternions produce the same rotation, and are therefore able to produce the 'three dimensional' space of three dimensional rotations.

[angeldude]

Quaternions are a 4D vector space of 3D rotations. 3 of the basis rotations are 180° (one for each plane/axis), and the remaining basis rotation is 0°. Ultimately, they're still best visualized as a single 3D rotation. (Obviously a weighted sum of 3D rotations yields another 3D rotation.)

P.S. The square root of a quaternion is just the average between itself and the 0° rotation, which is just a special case of a (normalized) weighted sum of rotations.

[markviz]

Just because a parabola uses 3 terms to be represented does not make it 3d, it has 3 terms but is an equation in 2 variables x and y which can be represented in 2D space for x and y being perpendicular, the same is true of quaternions. While I see what you’re saying, they technically exist in 4 perpendicular dimensions

[acykablyatley]

but they describe four dimensional rotations too, the three dimensional rotations they describe are a special case in the domain of their conjugate pairs...

[samuelbevins]

But parabolas form a 3D vector space? Aren’t the quaternions simply a 4D skew field satisfying all the properties of a 4D vector space?

[sebvv]

In the 2nd line you are adding a skalar to a vector. How does that work?

[pXnTilde]

ax^2 + bx + c does not describe a parabola. y = ax^2 + bx + c does. It's two dimensional because it has two dimensional variables, x and y.

[micahcrenwelge]

to describe a 3 dimensional object you only need 3 dimensions. in order to describe a TRANSFORMATION of a 3d object I think it is necessary to have a 4th dimension. Otherwise there is no meaningful transformation at all. Kind of like how time is considered a 4th dimension in our 3 dimensional world.

[egor.okhterov]

Dimension is the degree of freedom. Something that's independent. The quaternion lives in 4 dimensions, but when projected onto 3d space it gains power.

[tropin_tropin]

Kind of like in machine learning the weights associated with a sample x_1, …, x_n are w_1, …, w_n and the bias b