AP Calculus AB 4.2 Rectilinear Motion: Velocity, Acceleration, and Change of Direction

In AP Calculus AB, Section 4.2 focuses on **rectilinear motion**, emphasizing the relationships between velocity, acceleration, and change of direction. This section is crucial for understanding how objects move along a straight line and the mathematical principles underlying that motion. Here’s a detailed overview of these concepts:

### Key Concepts:

1. **Velocity**:
- Velocity is defined as the rate of change of an object’s position with respect to time. It is represented as the derivative of the position function, \( s(t) \):
\[
v(t) = s'(t)
\]
- Velocity can be positive or negative, indicating the direction of motion:
- A positive velocity indicates that the object is moving in the positive direction (to the right).
- A negative velocity indicates that the object is moving in the negative direction (to the left).
- When the velocity is zero, the object is momentarily at rest, which may suggest a change in direction.

2. **Acceleration**:
- Acceleration is defined as the rate of change of velocity with respect to time. It is represented as the derivative of the velocity function, \( v(t) \):
\[
a(t) = v'(t) = s''(t)
\]
- Acceleration can also be positive or negative:
- A positive acceleration means the object is speeding up in the positive direction or slowing down in the negative direction.
- A negative acceleration indicates the object is slowing down in the positive direction or speeding up in the negative direction.

3. **Change of Direction**:
- An object changes direction when its velocity changes sign. This occurs at points where the velocity function equals zero:
\[
v(t) = 0
\]
- To determine whether a change of direction occurs, students examine the intervals around these points:
- If the velocity changes from positive to negative, the object is changing direction from moving right to moving left.
- If the velocity changes from negative to positive, the object is changing direction from moving left to moving right.
- The acceleration at the point of change can also provide insight into the motion. A change in sign of acceleration at the point where velocity is zero indicates whether the object is transitioning from speeding up to slowing down or vice versa.

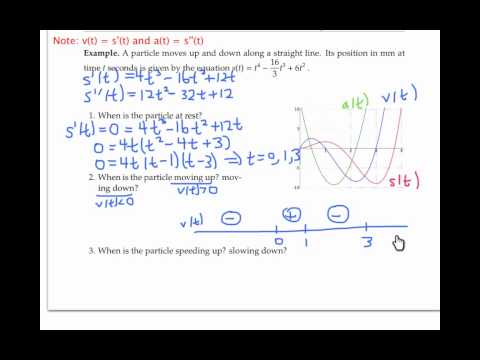
4. **Example Problem**:
- Consider a position function defined as \( s(t) = t^3 - 6t^2 + 9t \):
- To find the velocity, compute:
\[
v(t) = s'(t) = 3t^2 - 12t + 9
\]
- To find the acceleration, compute:
\[
a(t) = v'(t) = s''(t) = 6t - 12
\]
- Set the velocity function equal to zero to find critical points:
\[
3t^2 - 12t + 9 = 0
\]
- Analyze the intervals around the critical points to determine when the object is moving left or right and to identify any changes in direction.

5. **Graphical Interpretation**:
- Graphs of the position, velocity, and acceleration functions provide visual representations of motion:
- The position graph shows how the object moves over time, indicating where it is located at different points.
- The velocity graph reveals the direction and speed of the object, with changes in sign indicating changes in direction.
- The acceleration graph shows how the speed is changing over time, helping to determine whether the object is speeding up or slowing down.

### Applications:
- Understanding the relationships between velocity, acceleration, and direction is essential in physics and engineering contexts where motion is analyzed.
- Students can apply these concepts to real-world scenarios, such as vehicle dynamics and the motion of projectiles.

### Summary:
In Section 4.2 of AP Calculus AB, students delve into the concepts of velocity, acceleration, and change of direction in rectilinear motion. By analyzing the position, velocity, and acceleration functions, students develop a comprehensive understanding of how objects move along a straight line. This section equips them with the skills to mathematically and graphically analyze motion, setting the foundation for more advanced topics in calculus and its applications in the physical world.

I have many informative videos for Pre-Algebra, Algebra 1, Algebra 2, Geometry, Pre-Calculus, and Calculus. Please check it out:

/ nickperich

Nick Perich
Norristown Area High School
Norristown Area School District
Norristown, Pa

#math #algebra #algebra2 #maths #math #shorts #funny #help #onlineclasses #onlinelearning #online #study