AP Calculus AB 4.2 Rectilinear Motion: Finding where an Object is Speeding Up

In AP Calculus AB, Section 4.2 also covers how to determine when an object is speeding up or slowing down during rectilinear motion. Understanding these concepts is essential for analyzing the dynamics of an object's movement along a straight path. Here’s a detailed overview of how to find when an object is speeding up:

### Key Concepts:

1. **Position, Velocity, and Acceleration**:
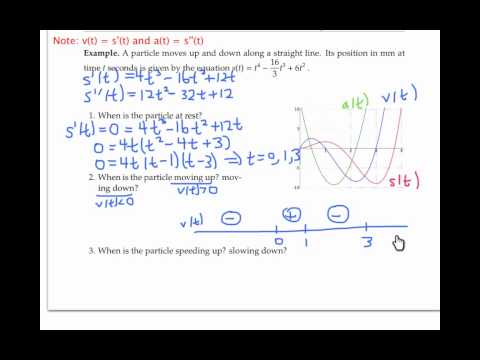
- As a reminder, the motion of an object is represented by a position function \( s(t) \), where \( s \) denotes the position and \( t \) denotes time.
- The velocity \( v(t) \) is the first derivative of the position function:
\[
v(t) = s'(t)
\]
- The acceleration \( a(t) \) is the derivative of the velocity function or the second derivative of the position function:
\[
a(t) = v'(t) = s''(t)
\]
- The signs of both the velocity and acceleration functions are crucial in determining whether the object is speeding up or slowing down.

2. **Speeding Up vs. Slowing Down**:
- An object is considered to be **speeding up** when both the velocity and acceleration have the same sign (either both positive or both negative).
- Conversely, the object is **slowing down** when the velocity and acceleration have opposite signs (one is positive, and the other is negative).

3. **Analyzing the Signs**:
- To find intervals where the object is speeding up, students should:
1. Calculate the velocity function \( v(t) \) and identify where it is positive or negative.
2. Calculate the acceleration function \( a(t) \) and determine its sign.
3. Analyze the intervals of \( t \) where \( v(t) \) and \( a(t) \) are both positive or both negative.

4. **Example Problem**:
- Consider a position function \( s(t) = t^3 - 6t^2 + 9t \):
- First, find the velocity:
\[
v(t) = s'(t) = 3t^2 - 12t + 9
\]
- Next, find the acceleration:
\[
a(t) = v'(t) = s''(t) = 6t - 12
\]
- Determine the critical points for both velocity and acceleration:
- Set \( v(t) = 0 \) and solve for \( t \).
- Set \( a(t) = 0 \) and solve for \( t \).
- Use the critical points to test the sign of \( v(t) \) and \( a(t) \) in the intervals defined by those points.
- Identify the intervals where both \( v(t) \) and \( a(t) \) are positive or both are negative, indicating that the object is speeding up.

5. **Graphical Interpretation**:
- Students can also use graphs to visualize the motion. The velocity graph shows the direction of movement, while the acceleration graph indicates whether the object is gaining speed (speeding up) or losing speed (slowing down).
- If both graphs are above the x-axis, the object is speeding up in the positive direction. If both are below the x-axis, the object is speeding up in the negative direction.

### Applications:
- Understanding when an object is speeding up is critical in various real-world applications, such as vehicle acceleration, projectile motion, and robotics.
- This knowledge helps students analyze dynamic systems and make predictions about the behavior of moving objects.

### Summary:
In Section 4.2 of AP Calculus AB, students learn how to find when an object is speeding up during rectilinear motion. By analyzing the signs of velocity and acceleration, they develop essential skills for interpreting motion and its dynamics mathematically. This section emphasizes the importance of understanding how different components of motion interact, laying the groundwork for more advanced topics in calculus and its applications in the physical world.

I have many informative videos for Pre-Algebra, Algebra 1, Algebra 2, Geometry, Pre-Calculus, and Calculus. Please check it out:

/ nickperich

Nick Perich
Norristown Area High School
Norristown Area School District
Norristown, Pa

#math #algebra #algebra2 #maths #math #shorts #funny #help #onlineclasses #onlinelearning #online #study