Related Rates in Calculus

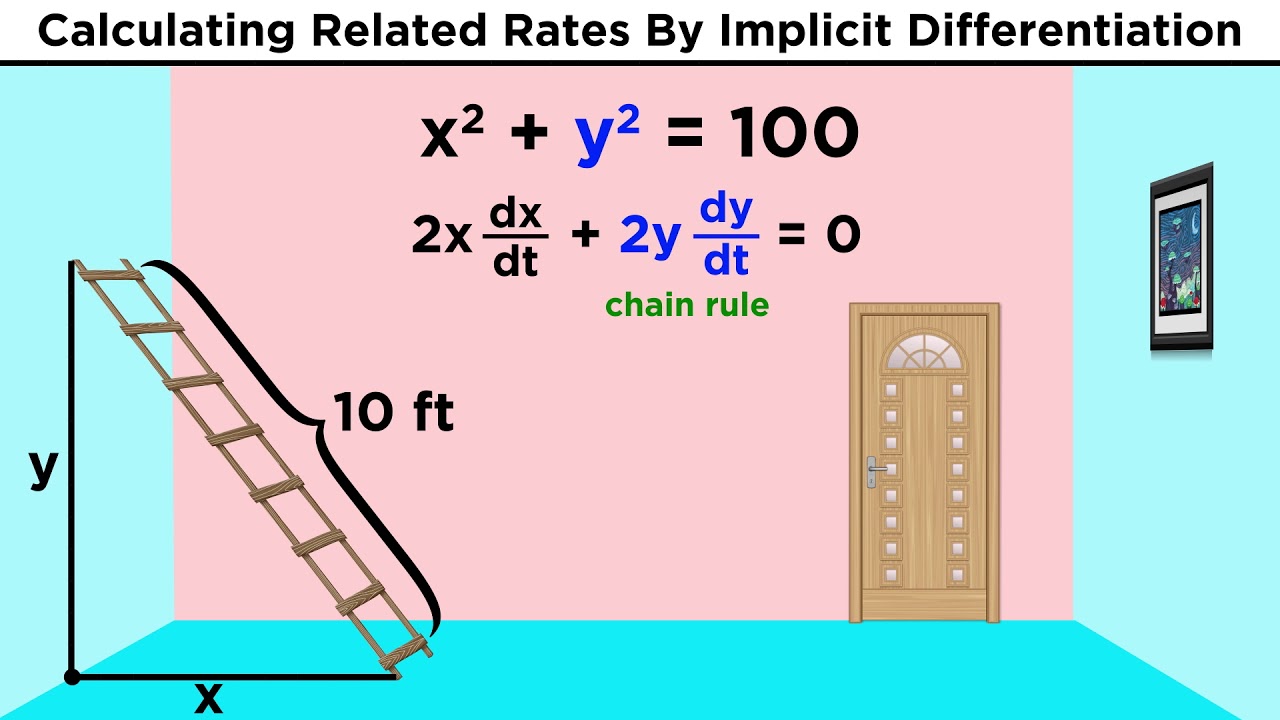
Now that we understand differentiation, it's time to learn about all the amazing things we can do with it! First up is related rates. Sometimes the rates at which two parameters change are related to one another by some equation. With our newfound understanding of implicit differentiation, it's not too hard to find this precise relationship so that we can do important scientific calculations. Check it out!

Check out "Is This Wi-Fi Organic?", my book on disarming pseudoscience!

[final]

I'm a college student, this is one of the best math explanations videos I've seen in my life. Great Job

[annas]

You saved me. This makes so much sense. Usually my math teacher is great at explaining, but I could not get related rates for the life of me. I can't believe it makes sense.

[Amit-yfft]

You are incredible. Some feedback: I love how you speak clearly and slowly. You pause at the best times so that we can process and take notes. You explicitly explain not only the process, but WHY and HOW this all makes mathematical sense. Thank you so much. My AP Calc teacher is amazing, she really is. It's just that after a long day at school it is hard to remember and process everything. I view this as a supplement to my learning process in Calculus (one of my favorite classes)

[onyxignites]

3:29

For anyone wondering, there is an alternative way of solving this problem. Instead of isolating "(dr / dt), " you could have simply plugged in the values there, which would have given you *100 = 4π[25^(2)] (dr / dt), * which simplifies to *100 = 2, 500π (dr / dt).* Isolating (dr / dt) gives you *(100 / 2, 500π) cm./sec., * which simplifies to *(1 / 25π) cm./sec.*

PS: I had to comment this on an alternative account because Dave blocked my main account from commenting on his channel.

[harshsinghal]

This is probably the only channel where one can want to continue learning new concepts. Waiting for the next.

[arthursodsod]

I've never been so nervous my whole life about an examination (which is tomorrow). This video will definitely help me pull through. I almost got the question by the end right (forgot to answer with the unit of measurement, but I got the numbers right, which is a feat for me). Hope I'll pass this first year as a college student. Thanks!

[schlck]

I know it's been 6 years but I just wanted to let you know how much these videos have been helping me recently. Thank you for making this easier to understand!

[DBear]

I took AP calc BC my senior year in high school. I failed calc 2 freshman year of college, so I'm retaking calc 1 and 2 this year. In high school, related rates were so complicated and stressful, so I was dreading doing them again this year. After watching this video, I had the problem done in maybe 2 minutes. Great video, very clear and helpful. You're doing God's work Dave! :D

[livbensen]

this video saved my life. I have a test for calc in about 5 hours and i feel much more confident. thank you!

[ScratRedemption]

Mathematics has always fascinated me from a statistical standpoint, as certain topics are learned much quicker to some vs others. For example, in my calculus class this most recent fall, my entire class had trouble with related rates but mastered optimization. I was the sole student where that was the opposite; Related rates were easy, optimization was not. When you get to calculus-difficulty in math, there isnt really a "best student", as some people can pick up on topics easier than others, so my advice to those that are struggling is to make lots of contacts in class to find out who picks up on what the fastest, and in case you are that person, to help others in your class.

[topsprout]

Why did this one video make more sense than the two weeks we spent on this topic in my AP Calc class?? You might've just saved my test grade tomorrow.

[CarsonG]

My differential calculus final is in 15 minutes. This was the only thing I was struggling with, and its been about a third of the class! Now I think I finally understand it!

[ATorres]

You make me actually want to apply related rates in real life. Thank you for keeping the material simple and sensible! 😃

[alexh]

What really made related rates click for me was realizing what we're differentiating with respect to when we solve a problem. What I mean is that I was used to d/dx, but with a related rate problem, you're differentiating X and Y with respect to time. So rather than dy/dx and dx/dx, it's dy/dt and dx/dt

[alvideor]

What does it mean to have dV or dr or dt just on its own and not in a derivative fraction?

Here is what I mean. First example can also be solved like this:
dV/dr = 4pi*r^2 --> dV = 4pi*r^2 * dr
dV/dt = 100 --> dV = 100*dt
4pi*r^2 * dr = 100*dt
dr/dt = 100/(4pi*r^2) etc

My question is, what is actually happening when the separate d terms start bouncing around in the expressions? Are they just infinitesimal changes in a variable? It's strange that they can be split off from derivative fractions and recombined to form a different derivative.

[__lunareclipse]

This is a really great explanation, neat, and much better than my teacher. Thank you!

[classifiesconfidential]

The sliding ladder is my grade in calculus.

[Dusk]

This video is fantastic. I could not grasp this concept in class but this was simple and easy to understand. Your work is legendary.

[hanaadil]

THANK YOU SO MUCH. PLEASE KEEP DOING WHAT YOU'RE DOING!

[kingsleynnadi]

Im a highschool student having calculus trouble but these videos really help alot 😀 Thanks Professor Dave.