AP Calculus AB 4.2 Rectilinear Motion: Finding Velocity and Acceleration

In AP Calculus AB, Section 4.2 focuses on rectilinear motion, specifically how to find velocity and acceleration from a function that describes the position of an object over time. This section introduces key concepts related to motion along a straight line and emphasizes the relationship between position, velocity, and acceleration. Here’s an overview of the key concepts and methods covered in this section:

### Key Concepts:

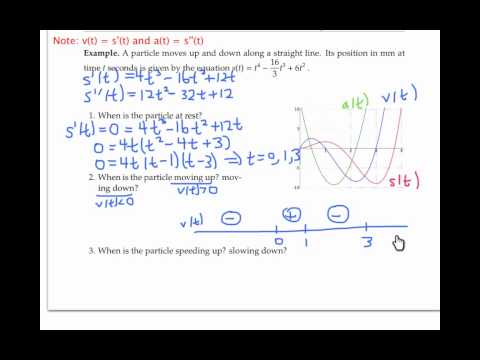
1. **Position Function**:
- The position of an object moving along a straight line can be represented by a function \( s(t) \), where \( s \) is the position in a given unit (such as meters) and \( t \) represents time (in seconds).
- This function describes the location of the object at any given moment.

2. **Velocity**:
- The velocity of an object is the rate of change of its position with respect to time. Mathematically, velocity is defined as the first derivative of the position function:
\[
v(t) = s'(t)
\]
- The velocity function \( v(t) \) indicates how fast and in what direction the object is moving at time \( t \).
- If \( v(t) \) is positive, the object is moving in the positive direction. If \( v(t) \) is negative, the object is moving in the negative direction.

3. **Acceleration**:
- Acceleration is the rate of change of velocity with respect to time. It can be expressed as the derivative of the velocity function or the second derivative of the position function:
\[
a(t) = v'(t) = s''(t)
\]
- The acceleration function \( a(t) \) describes how the velocity of the object is changing over time.
- Positive acceleration indicates an increase in velocity, while negative acceleration (deceleration) indicates a decrease in velocity.

4. **Interpreting Graphs**:
- The position, velocity, and acceleration can be graphed to visualize the motion of the object.
- The slope of the position graph at any point gives the velocity at that point, while the slope of the velocity graph provides the acceleration.
- Understanding these relationships helps analyze the motion of the object more thoroughly.

5. **Example Problem**:
- Given a position function such as \( s(t) = t^3 - 6t^2 + 9t \):
- To find the velocity, calculate \( v(t) = s'(t) = 3t^2 - 12t + 9 \).
- To find the acceleration, calculate \( a(t) = v'(t) = s''(t) = 6t - 12 \).
- By analyzing the velocity and acceleration functions, students can determine the object's speed, direction, and changes in motion over time.

### Applications:
- Understanding rectilinear motion is essential for solving problems in physics and engineering, where motion along a straight path is analyzed.
- Students apply these concepts to real-world scenarios, such as objects in free fall, vehicles on a straight road, or projectiles in motion, enhancing their ability to model and predict motion mathematically.

### Summary:
Section 4.2 of AP Calculus AB lays the groundwork for understanding rectilinear motion through the relationships between position, velocity, and acceleration. By mastering these concepts and their mathematical representations, students gain valuable skills for analyzing motion, preparing them for more complex topics in calculus and physics.

I have many informative videos for Pre-Algebra, Algebra 1, Algebra 2, Geometry, Pre-Calculus, and Calculus. Please check it out:

/ nickperich

Nick Perich
Norristown Area High School
Norristown Area School District
Norristown, Pa

#math #algebra #algebra2 #maths #math #shorts #funny #help #onlineclasses #onlinelearning #online #study