filmov
tv
This Result Keeps Me Up At Night

Показать описание
What is the sum of all the natural numbers?! Of course the answer is obvious...right? Many have actually pointed to the result that the sum of natural numbers is negative 1/12 !
We're going to do a 1+2+3+...=-1/12 proof , then a false sum of all natural numbers proof. What can we make of this?!
►BECOME A CHANNEL MEMBER
►WEBSITE
Disclaimer: This video is for entertainment purposes only and should not be considered academic. Though all information is provided in good faith, no warranty of any kind, expressed or implied, is made with regards to the accuracy, validity, reliability, consistency, adequacy, or completeness of this information.
1+2+3+4+5+6+n=-1/12 proof
#math #brithemathguy #sumofallnaturalnumbers
This Result Keeps Me Up At Night
This Fact Keeps Me Up At Night
This Game Keeps Me Up At Night
This Result Keeps Me Up at Night...
She Keeps Me up - Nickelback Lyrics
Nickelback She Keeps Me Up Official Video
Michael Schulte - Keep Me Up (Official Lyric Video)
Give me everything u took from me keep u-up on my chance on the my chance
Top 10 Things That Keep Me Awake at Night
She Keeps Me Up
B.I Keep me up Lyrics (Color Coded Lyrics)
Thanks for all the love for 'She Keeps Me Up'. That one was pretty unexpected!
Michael Schulte - Keep me up (Lyrics / Lyric Video)
Nickelback - She Keeps Me Up
Charlotte Lawrence - Keep Me Up (Official Music Video)
Scary TikTok That Keep Me Up At Night #61
She Keeps Me Up - Nickelback
Scary TikToks That Keep Me Up At Night #33
THE DRIVER ERA - You Keep Me Up at Night (Official Video)
She Keeps Me Up - Yor Edit [SPY X FAMILY]
Nightcore - She Keeps Me Up
Nickelback - She Keeps Me Up (Traducción al español)
Historical Mysteries That Keep Me Up At Night
Michael Schulte - Keep Me Up - | ZDF-Fernsehgarten
Комментарии
 0:08:53
0:08:53
 0:03:48
0:03:48
 0:04:53
0:04:53
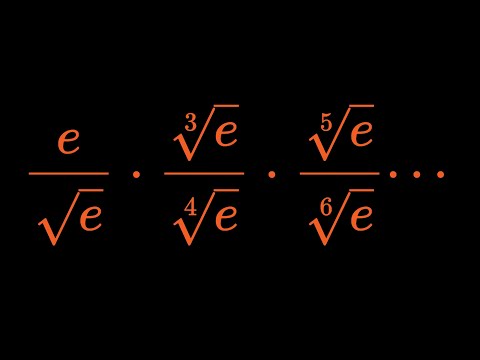 0:16:16
0:16:16
 0:03:58
0:03:58
 0:04:43
0:04:43
 0:02:54
0:02:54
 0:00:16
0:00:16
 0:06:48
0:06:48
 0:03:58
0:03:58
 0:03:26
0:03:26
 0:00:13
0:00:13
 0:02:53
0:02:53
 0:04:00
0:04:00
 0:03:20
0:03:20
 0:09:30
0:09:30
 0:00:08
0:00:08
 0:08:04
0:08:04
 0:02:20
0:02:20
 0:00:27
0:00:27
 0:03:22
0:03:22
 0:03:58
0:03:58
 0:43:27
0:43:27
 0:04:29
0:04:29