filmov
tv
Number Theory | Sums of Squares Part 4

Показать описание
We provide a few examples of writing natural numbers as sums of two squares.
Number Theory | Sums of Squares Part 1.
Number Theory | Linear Congruence Example 2
two number theory problems
A nice and quick elementary number theory problem.
Problem Solving | Techniques from Number Theory
Why greatest Mathematicians are not trying to prove Riemann Hypothesis? || #short #terencetao #maths
A throwback number theory problem
5 simple unsolvable equations
Olympiad Mathematics | High School Students Can Solve It
Top ten open problems in Number Theory
4 Relaxing Number Theory Problems.
What does a ≡ b (mod n) mean? Basic Modular Arithmetic, Congruence
A cool number theory problem!
The High Schooler Who Solved a Prime Number Theorem
The Most Efficient Way for Beginners to Start Understanding Number Theory!
probably a number theory problem.
This completely changed the way I see numbers | Modular Arithmetic Visually Explained
Math in a snowstorm!! -- a nice number theory problem.
Number Theory: Queen of Mathematics
Number Theory | Divisibility Basics
IMO, a Very Nice Number Theory Exercise.
A number theory proof
Number Theory | Chinese Remainder Theorem: Example 4
A Big Secret in Solving Number Theory Problems | Turkish Junior Mathematical Olympiad 2012 P1
Комментарии
 0:06:37
0:06:37
 0:04:44
0:04:44
 0:09:44
0:09:44
 0:09:44
0:09:44
 0:28:27
0:28:27
 0:00:38
0:00:38
 0:11:13
0:11:13
 0:00:50
0:00:50
 0:07:52
0:07:52
 0:06:35
0:06:35
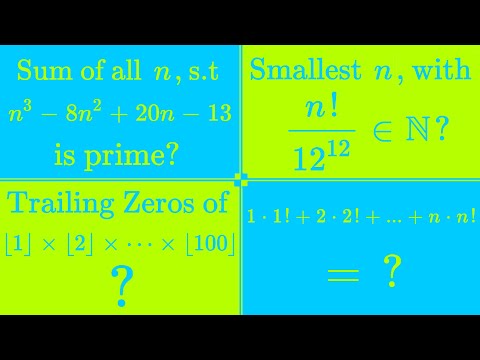 0:21:13
0:21:13
 0:05:45
0:05:45
 0:10:41
0:10:41
 0:05:15
0:05:15
 0:02:29
0:02:29
 0:09:34
0:09:34
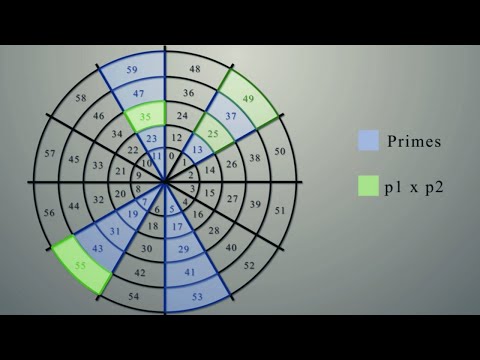 0:20:33
0:20:33
 0:05:53
0:05:53
 1:02:35
1:02:35
 0:07:13
0:07:13
 0:23:19
0:23:19
 0:10:17
0:10:17
 0:07:15
0:07:15
 0:06:27
0:06:27