filmov
tv
Problem Solving | Techniques from Number Theory

Показать описание
We look a few concepts and results from Number Theory that are commonly used in mathematics competitions. Solutions to two examples are also given, including one to the 1985 AIME.
If you are going to use an ad-blocker, considering using brave and tipping me BAT!
Books I like:
Abstract Algebra:
Differential Forms:
Number Theory:
Analysis:
Calculus:
My Filming Equipment:
If you are going to use an ad-blocker, considering using brave and tipping me BAT!
Books I like:
Abstract Algebra:
Differential Forms:
Number Theory:
Analysis:
Calculus:
My Filming Equipment:
SHARPEN YOUR ANALYTICAL AND PROBLEM SOLVING SKILLS
Clarifying the '5 Whys' Problem-Solving Method
How to Solve a Problem in Four Steps: The IDEA Model
Problem-Solving for Developers - A Beginner's Guide
Improve Your Problem Solving Skills
Problem Solving Techniques - For Programming Problems & Interviews
5 Step Formula to Solve Any Problem | Brian Tracy
HOW TO SOLVE PROBLEMS - How do consulting firms work (hypothesis-based problem solving explained)
CAT 23 DILR 90%ile set - Key skills Vs Problem Solving
4 Steps in Solving Problems
Working backward to solve problems - Maurice Ashley
Tips to be a better problem solver [Last live lecture] | Ep. 10 Lockdown live math
How to Awaken & Enhance Your Analytical Problem-Solving Mind
The Ultimate Problem–Solving Strategy | My Secret to Winning Physics, Math, and Coding Competitions...
Problem Solving Skills | How to Improve Your Problem Solving Skills? | Softskills | Simplilearn
Problem Solving Techniques: 5-Why-Method, Flowchart, Mind-Map
The 5 Whys of Problem-Solving Method
PROBLEM-SOLVING Interview Questions and ANSWERS!
Learn Toyota's 8 Step Practical Problem Solving Methodology
What is Problem Solving | Explained in 2 min
Problem Solving Strategy: 7 Steps of the ‘Fish Technique’
Problem Solving: 6 Skills needed to solve any problem
The surprising secret that solves your problems quickly | Collins Key | TEDxSantaBarbara
5 tips to improve your critical thinking - Samantha Agoos
Комментарии
 0:08:19
0:08:19
 0:03:20
0:03:20
 0:05:23
0:05:23
 0:10:44
0:10:44
 0:03:33
0:03:33
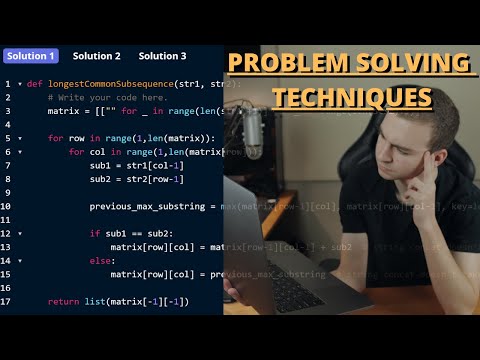 0:17:40
0:17:40
 0:07:29
0:07:29
 0:11:07
0:11:07
 0:21:23
0:21:23
 0:03:50
0:03:50
 0:05:57
0:05:57
 1:08:20
1:08:20
 0:22:45
0:22:45
 0:16:19
0:16:19
 0:08:09
0:08:09
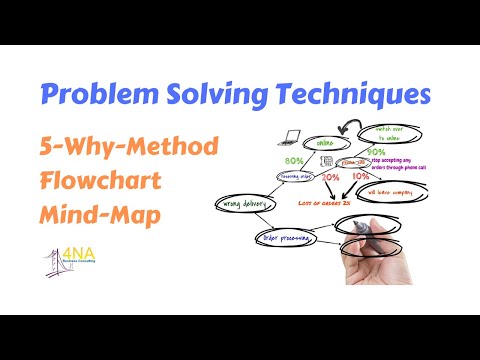 0:08:59
0:08:59
 0:02:03
0:02:03
 0:07:26
0:07:26
 0:10:49
0:10:49
 0:02:33
0:02:33
 0:02:29
0:02:29
 0:02:20
0:02:20
 0:15:25
0:15:25
 0:04:30
0:04:30