filmov
tv
4 Relaxing Number Theory Problems.

Показать описание
Today we take a look at 4 relaxing number Theory problems I found over on Brilliant :) Featuring factorial, a Diophantine equation and a sneaky little identity. Enjoy! =D Video sponsored by Brilliant btw :)
Help me create more free content! =)
--------------------------------------------------------------------------------
Wanna send me some stuff? lel:
Postfach 11 15
06731 Bitterfeld-Wolfen
Saxony-Anhalt
Germany
--------------------------------------------------------------------------------
0:00 Intro
1:35 Solution 1
8:50 Solution 2
12:37 Solution 3
15:26 Solution 4
4 Relaxing Number Theory Problems.
A little Number Theory for Relaxation
A nice problem for Number Theory
Math isn't actually Sorcery ✨🪄 #terencetao #mathematics
Math Major Examples — Number Theory #1
Peter Sarnak - Patterns in Number Theory - Misleading or True? - SUMS 2021 Math and Illusion
One number theory problem for beginners
An IMO shortlisted problem | Number Theory Problems
[4] Number Theory | a divides b: Which integers divide zero?
Popular Olympiad problems | Number Theory
ASMR Teaching You Math | Number Theory | Intro to Euler's Totient Function *Softspoken*
Ramanujan's Magnificent Formula For π #ramanujan #mathematics #maths
IIT Bombay Lecture Hall | IIT Bombay Motivation | #shorts #ytshorts #iit
Math olympiad | Number Theory | What is the remainder when 1+2+3+... + 2023 is divided by 1000 ?
[ASMR Math] Number Theory- Chinese Remainder Theorem Example | Clicky Breathy Whispering, Writing
Number Theory Midterm I - Segment 1
Factoring large numbers into primes | Famous Math Problems 1 | NJ Wildberger
This chapter closes now, for the next one to begin. 🥂✨.#iitbombay #convocation
#maths #challenge #mathematics #gk #gkshorts #shorts #funny #viral
Math Olympiad Preparation | A Nice Factorial Problem | Calculate Without Calculators...
ASMR Math | Number Theory- Euler’s Totient Function (Whisper, Softspoken, Educational, Teaching You)...
A Nonstandard Equation
How to Become an Alpha Chad Engineer.
Number Theory Lecture from 4-16-2015
Комментарии
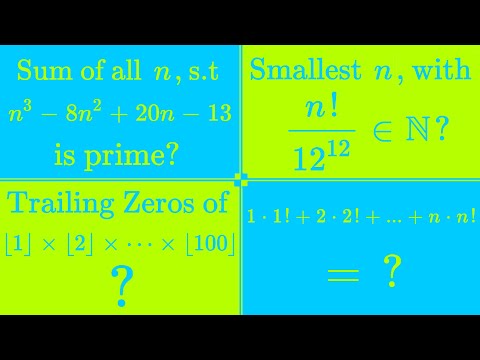 0:21:13
0:21:13
 0:03:01
0:03:01
 0:05:29
0:05:29
 0:00:42
0:00:42
 0:15:50
0:15:50
 1:15:55
1:15:55
 0:04:41
0:04:41
 0:04:55
0:04:55
![[4] Number Theory](https://i.ytimg.com/vi/N6hwaesdCPM/hqdefault.jpg) 0:15:28
0:15:28
 0:03:45
0:03:45
 0:34:39
0:34:39
 0:00:37
0:00:37
 0:00:12
0:00:12
 0:01:34
0:01:34
![[ASMR Math] Number](https://i.ytimg.com/vi/swpyhFtdhnY/hqdefault.jpg) 0:26:52
0:26:52
 0:29:51
0:29:51
 0:42:03
0:42:03
 0:00:16
0:00:16
 0:00:05
0:00:05
 0:06:19
0:06:19
 0:27:17
0:27:17
 0:08:55
0:08:55
 0:00:47
0:00:47
 1:14:02
1:14:02