filmov
tv
Calculus 2 - Integration: Finding the Area Between Curves (13 of 22) Finding the Limits of Integral

Показать описание
In this video I will find the area between the 2 functions y1=x^3, and y2=x.
Next video in this series can be seen at:
Calculus 2 - Basic Integration
Finding the Area Between Two Curves by Integration
Calculus 2 - Integration: Finding the Area Between Curves (13 of 22) Finding the Limits of Integral
Calculus 2 - Integration: Finding the Area Between Curves (12 of 22) Horizontal dA
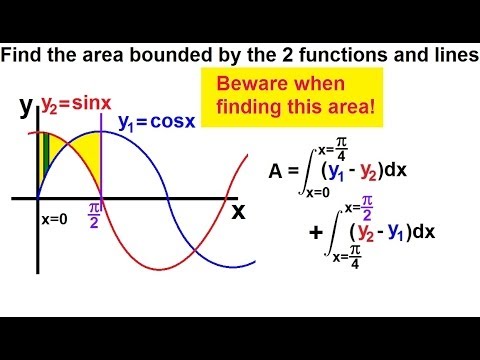
Calculus 2 - Integration: Finding the Area Between Curves (3 of 22) Ex. 3: y=sinx, y=cosx BEWARE!
Calculus 2 - Integration: Finding the Area Between Curves (11 of 22) Area of a Sector
Integration (Calculus)
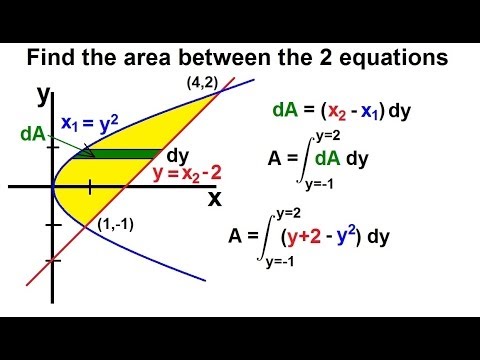
Calculus 2 - Integration: Finding the Area Between Curves (4 of 22) Ex. 4: x=y^2, y=x-2
Calculus NCEA Level 2 in 15 hours | Part 3
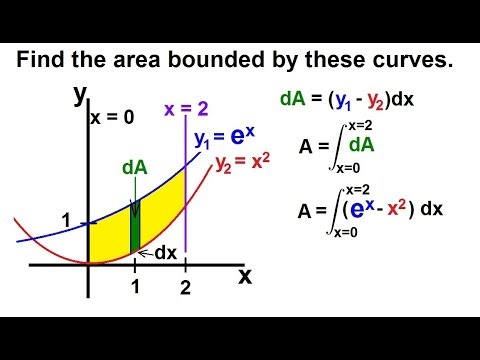
Calculus 2 - Integration: Finding the Area Between Curves (1 of 22) Ex. 1: y=e^x, y=x^2, x=0, x=2
Find the centroid, calculus 2
Calculus 2 - Integration: Finding the Area Between Curves (19 of 22) 3 Curves
Calculus 2 - Integration: Finding the Area Between Curves (17 of 22) Trigonometric Functions: Ex. 1
What Integration Technique Should I Use? (trig sub, u sub, DI method, partial fractions) calculus 2
Calculus 2 - Integration: Finding the Area Between Curves (8 of 22) Example 8: Method 1 of 3
calculating work by using integral, pumping water out of a tank, calculus 2 tutorial
Calculus 2 - Integration: Finding the Area Between Curves (10 of 22) Example 8: Method 3 of 3
Calculus 2 - Integration: Finding the Area Between Curves (16 of 22) Without Symmetry
Calculus 2 - Integration: Finding the Area Between Curves (5 of 22) Ex. 5: y=(1/4)x^2, y=x
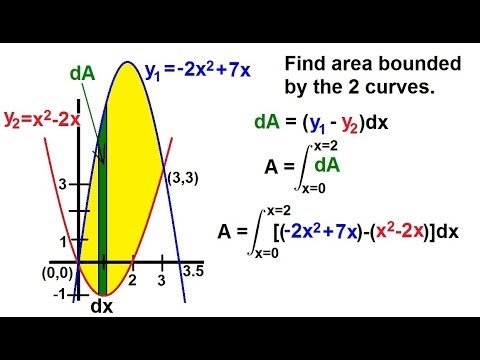
Calculus 2 - Integration: Finding the Area Between Curves (2 of 22) Ex. 2: y=(x^2)-2x, y=-(2x^2)+7x
Finding The Area Under The Curve Using Definite Integrals - Calculus
Work Problems | Calculus 2 Lesson 8 - JK Math
Calculus 2 - Integration: Finding the Area Between Curves (20 of 22) Exponential Functions: Ex. 1
Calculus 2 - Integration: Finding the Area Between Curves (18 of 22) Trigonometric Functions: Ex. 2
Комментарии
 0:26:12
0:26:12
 0:07:52
0:07:52
 0:05:05
0:05:05
 0:05:42
0:05:42
 0:08:43
0:08:43
 0:08:04
0:08:04
 0:07:04
0:07:04
 0:08:14
0:08:14
 1:08:10
1:08:10
 0:06:13
0:06:13
 0:07:36
0:07:36
 0:06:54
0:06:54
 0:09:13
0:09:13
 0:22:40
0:22:40
 0:06:59
0:06:59
 0:09:05
0:09:05
 0:02:45
0:02:45
 0:08:04
0:08:04
 0:05:17
0:05:17
 0:09:35
0:09:35
 0:34:24
0:34:24
 0:57:10
0:57:10
 0:03:14
0:03:14
 0:07:54
0:07:54