filmov
tv
calculating work by using integral, pumping water out of a tank, calculus 2 tutorial
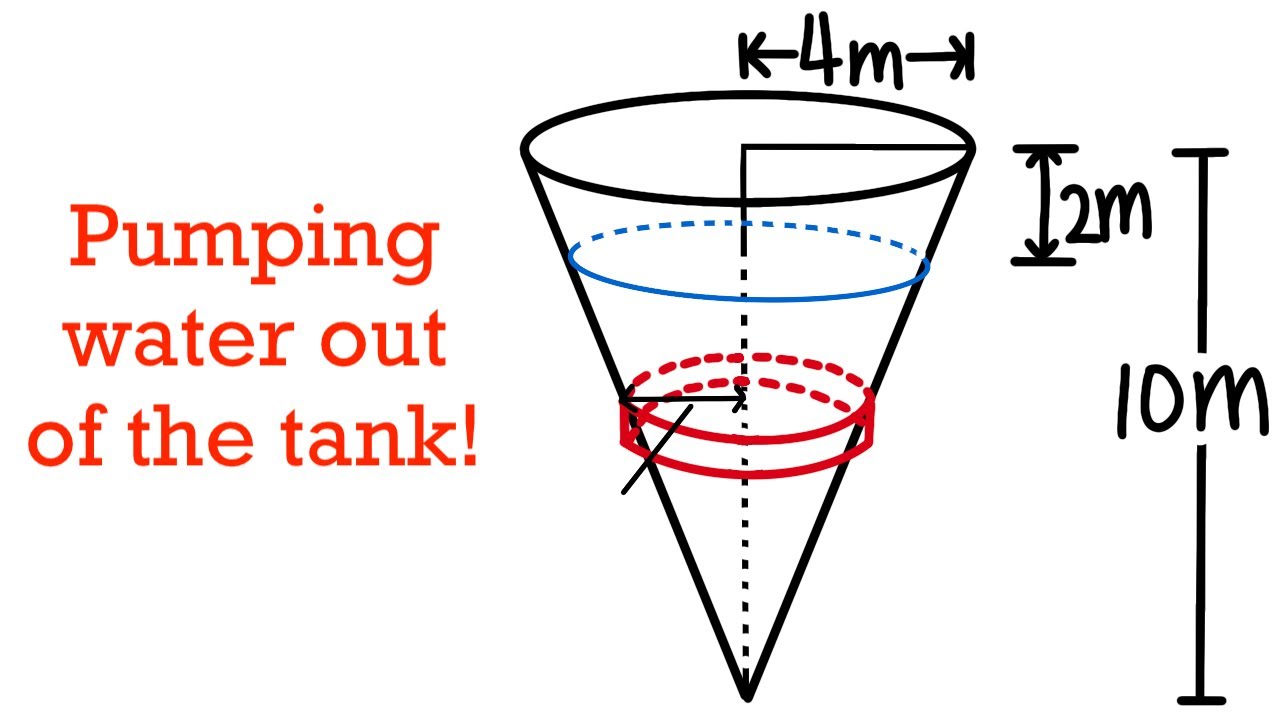
Показать описание
Application of integration. Calculating the work it needs to pump the water out of a conical tank. Calculus 2 tutorial.
----------------------------------------
#blackpenredpen #math #calculus #apcalculus
----------------------------------------
#blackpenredpen #math #calculus #apcalculus
calculating work by using integral, pumping water out of a tank, calculus 2 tutorial
Using a line integral to find the work done by a vector field example | Khan Academy
Integral Introduction via Work
How REAL Men Integrate Functions
Calculating Work to Empty a Spherical Tank - Integral Calculus
Example: Computing the Line Integral of a Vector Field (i.e. Work Done)
From Power to Work using an Integral - Example
Work Done Raising a Leaky Bucket with an Integral
Finding the Area Between Two Curves by Integration
Finding work done along straight line/ Line Integral problem a long straight line
Calculate the Work Done to Stretch a Spring Using a Definite Integral
Find The Integral – How To Do Basic Calculus Integration
What is Integration? Finding the Area Under a Curve
Work as an Integral
How to Evaluate the Line Integral of a Vector Field
How to Find a Definite Integral using Riemann Sums and the Limit Definition: Quadratic Example
Integration and the fundamental theorem of calculus | Chapter 8, Essence of calculus
Disk & Washer Method - Calculus
Introduction to integral calculus | Accumulation and Riemann sums | AP Calculus AB | Khan Academy
Mass of a Wire with Line Integral - Vector Calculus Application
Calculating Work for a Conical Tank with Definite Integral Ch6R15
Integrals: Crash Course Physics #3
Calculus 3: Line Integrals (18 of 44) What is a Line Integral? [(y)dx+(z)dy+(x)dz] Example 6
What does area have to do with slope? | Chapter 9, Essence of calculus
Комментарии
 0:09:05
0:09:05
 0:11:32
0:11:32
 0:18:31
0:18:31
 0:00:35
0:00:35
 0:08:37
0:08:37
 0:06:55
0:06:55
 0:04:54
0:04:54
 0:08:03
0:08:03
 0:07:52
0:07:52
 0:09:12
0:09:12
 0:03:31
0:03:31
 0:11:08
0:11:08
 0:08:18
0:08:18
 0:11:41
0:11:41
 0:06:16
0:06:16
 0:13:18
0:13:18
 0:20:46
0:20:46
 0:20:00
0:20:00
 0:04:52
0:04:52
 0:06:46
0:06:46
 0:06:16
0:06:16
 0:10:09
0:10:09
 0:05:03
0:05:03
 0:12:39
0:12:39