Trig identities and Euler's formula

Показать описание

This is the problem that we are going to look at. we are going to … we are asked to
apply this identity here between sinθ and these exponentials to express (sinθ)^4 in terms of
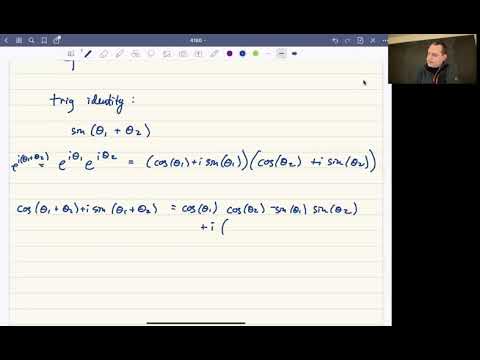
cosθ, cos2θ, etc. Euler’s formula e^(iθ) = cosθ + isinθ.
Now, we can manipulate that to make cosine and essentially sin the subject and come up with
these. So here cosine is written in terms of the exponentials, sine is written in terms of
exponentials. So where do these come from? Well let us think about, say *. Alright well if I go up
to Euler’s formula and replace θ with –θ; because cosine is an even function and sine is an odd
function, the right-hand side up here, that will become … cos(-θ) will go to cosθ and sin(-θ) will
go to –sinθ. Cosine is an even function and sin is odd.
So cos(-θ) = cosθ, sin(-θ) = -sinθ. If you add
this to this the isinθ’s will cancel out and you would be left with 2cosθ = e^(iθ) + e^-(iθ). So you
just take the 2 down there and you get cosθ on its own. Now, to get sinθ like this, we would take
the second equation away from the first. So that way, the cosθ’s will cancel and you will be left
with 2isinθ = e^(iθ) – e^-(iθ) and you would come up with that. 0:28 – 3:27.
So that is where they come from. How are they useful? Well, let us do the example and then I
will explain why it is important, or what its uses are. Let us start
and raise both sides to the power of 4. So let us call this I for Identity. This
is (sinθ)^4. We want to simplify this somehow, and then once you simplify it you want to connect
it back to something involving cosines: cosθ, cos2θ, cos3θ, etc. So what we are going to do is
expand this using Pascal’s Triangle. So Pascal’s triangle gives you a way of determining the
coefficients when you are doing an expansion like this. So you write down Pascal’s triangle by
adding 1’s down the sides and you add numbers together to get the ‘internal numbers’. Now this 2i down here, where i is the imaginary unit and i^2 = -1, that
can be treated separately so I am going to bring that out here. I will expand this part using
Pascal’s Triangle and I can simplify this essentially on it is own. So because i^2 = –1, i^4 = –1 x
–1 so that is just +1. 2^4 will be 16, so I can start … this is going to simplify to 1/16, and now all
I need to do is expand this expression using Pascal’s Triangle. So e^(iθ), I raise that to the
power of 4 and the coefficient is 1. Then I move on to this one. The coefficient is going to be 4. I
decrease this power by 1 and I increase the power of this term by 1. So that will be 1. Move on
to the next one. The coefficient is going to be 6. So now we can simplify what is here just by using the
exponent laws and power laws. So this 4 is going to come inside and you are going to get
e^(i4θ). Now this is going to be a 3θ, this is going to be a –θ. When you multiply these two
things together, you are going to get 3θ – θ, so you are going to get e^(i2θ) out of that. Same
over here, you are going to get a 2θ and a -2θ, and when you multiply those together, the power
is essentially going to drop out and so you are going to get 6. Over here you are going to get …
you have got a θ up there and a -3θ and when you combine those you are going to get a -2θ...
That will be a 3θ and that will be a –θ so you
will actually get a POSITIVE i2θ up there. Well this is going to
become e^-(i4θ) and the negative will become a positive because you are taking it to the power
of 4. Well we want to get back to something like cosθ or cos2θ
or cos3θ or something like that. Now from these expressions over here you can also see that if I
replace θ with nθ, with n being an integer, I get the following. So if you could put the brackets in
if you wanted to.And if I team this with this, take out negative signs, this is looking a lot like
this with n = 2. I just do not have the division by 2i. So I kind of know where I am going here. I
am sort of aiming for something involving cos4θ and cos2θ. Alright so let me expand on this a
little bit more. Okay well I can distribute that 1/16 with this 6 because the 6 is not going to
involve cos or anything. So that will give me 3/8. I have put a little 2 in there just so that
really is cos4θ, and what I can do with the remaining terms is I can do the following. Okay, I
have got the 16 over here, so if I divide the 16 into the 4 I will get 1/4 and then I can break that
1/4 into 1/2 x 1/2. So I have just played with it a little bit and I have got cos4θ there; I have got
cos2θ there so now I can basically write everything down in terms of … these sort of cosine
expressions.If we go back to this
left hand side you can now move that 4 in there of course and write it down. So here is your
identity. 3:27 – 13:30.