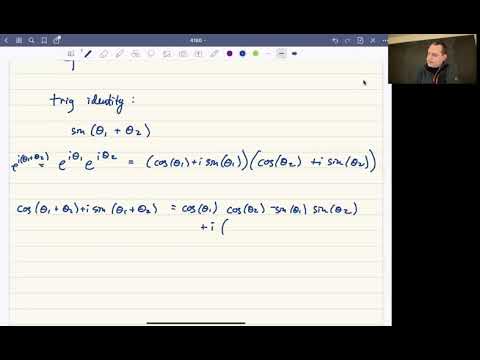
Euler's formula and trig identities

So let us start with, say, *, and I want (sinθ)^5 so let us take the … both sides and raise them to
the power 5. So from * we have the following. So basically I am just taking both sides to the
power of 5, and let us try to simplify this. we are going to have to expand it. Let me just switch to
a different-coloured pen for a second because this one is about to run out. Now I can expand
the top part using Pascal’s triangle. The bottom part can just be sort of moved out the front and
taken to the power of 5, so 2^5 is 32. i^5, ok so i^2 = –1, i^4 = –1 x –1 so that will be 1, so if I
bring this out the front I will get 1/32i, because i^5 is just i. Okay so how do I expand this? I have
got rid of that little bit there. let us use Pascal’s triangle. So Pascal’s triangle is something that
you would learn at high school and it tells you the coefficients for this type of expansion. So you
start with this, you add the numbers to get the corresponding; sort of, numbers below, and you
just keep going down till you have got down to the row that you want to get down to. Okay so
this is squared, cubed, power of 4, we want power of 5 so the next one. Alright so let us expand this out and see how we go. Okay so we have got this
1/32i, which I am going to leave alone. So this raised to the power 5, so that will be (e^iθ)^5 and
then using my exponent or index laws if you like, it will be e^(i5θ). Now what you do is you
decrease the power on this and you increase the power on this and you use this coefficient up
here. So I am going to get 5 times (e^iθ) all to the power 4 which is that, times this to the power
1, okay? And I will simplify this later. Then I will move on to the next one, so the coefficient is 10.
So instead of having power 4 associated with this, it will be power 3. So when I do that and use
the exponent laws it will be e^(i3θ) times all of this to the power 2 okay? you are increasing that,
so this will then be … I am squaring all this so the negative will become a positive. The (e^(–
iθ))^2 will become e^(–i2θ). So instead
of having a 3 here, we will have a 2 because that is going to decrease and here you are going to
get … we are cubing this so there will be a negative sign there, and you will get e^(–i3θ). Okay,
and second lastly, we have got 5 here so this will become decreased by 1, e^(iθ),
so we will be taking –e^(-iθ)) all to the power 4, so the negative sign will disappear and you will
be left with e^(–i4θ), and lastly, this will be taken all to the power 5, so you will get your negative
sign back and you will get something like that. You could take more than one line to do that. It just depends on how familiar you are
with Pascal’s triangle and the algorithms. 1:33 – 6:57
Let us do one more simplification here. So I have got e^(i5θ). So I have taken those
out. What about in here? If I use my index laws, or exponent laws, I will get e^(i3θ) out of this
and with a minus sign, so I will get this and over here I will get e^(–i3θ).
Okay, so they are taken care of, the 10’s, well they will team up as well. If I simplify these
exponents I will just be left with an iθ up there and a –iθ up there. So I can actually simplify that.
So that is going to give me 10e^(iθ), and this one is going to be –10e^(-iθ). Now why have I
teamed these up together? Well you will see that that is almost the same as cos5θ, I am just
missing the division by 2, okay? And this is essentially, almost the negative of 5 times … sorry,
sinθ. So this is almost sin5θ, this is almost sin3θ, and this is almost sinθ. So that is almost
sin5θ, that is almost sin3θ and that is almost sinθ. So if I distribute, say, 2i from here in there, I
will get, pretty much, exactly what I want here. Alright, so there we go. So that now is exactly
sin5θ, from here with n = 5. That is sin3θ and that is just sinθ, so now I can actually write
(sinθ)^5 in terms of these sort of parts. Okay so I have got sin5θ – 5sin3θ + 10sinθ. Okay so we
want this in terms of all this so let us actually write a conclusion there. Okay so I guess if I want
to I can distribute this in, and the common factor of 2, and there we have it. 6:57 – 11:30
Okay so a good question here is: ‘why would I want to do that? why would I want to express this
in terms of these things here?’ Well one way of motivating these kinds of problems is through
integration. So I know we are working with complex numbers here, but you can use these ideas
in integration. let us say you were asked to integrate this: (sinθ)^5 with respect to θ. If you know that you can express (sinθ)^5 in terms of these things, these
things are easy to integrate. You can integrate term-by-term and do it in essentially one line
here. So that is one of the motivations for using these kinds of identities.

[InnocentEX]

Mate your a legend, this is the best description of Euler's formula I've seen. Thank you for helping me to finally grasp this concept.

[TheJjackk]

Great man - I'm almost finished with all of your videos (started about five days ago) and this has taught me a lot. Good job and thanks!

[mickodillon]

what a beautiful piece of mathematics Euler's formula is. Still looking forward to that Tensors video Chris!

[Matchbox]

What happen to that Google Hangout video you made on De Moivre's  formula that started out discussing how to write cos 5 (theta) in terms of cos (theta)? I cant find it.

[Vipa]

can you do the opposite, like write sin 5theta in terms of powers?

[chandnibhudia]

can you please help me??? how to we begin to integrate |2e^(ix) - 1|^2 2ie^(ix) from [0, pi]!! ive done verything, used the identity z(z bar) = |Z|^2 but this is tedius!!! please anyone??? apparantly the answer is -8pi!! but my lectuere has not exaplied how!!