filmov
tv
Efficient Frontier, Utility and Portfolio Optimization

Показать описание
This video is free lecture on the application of Residual Income Model for equity valuation. Full lecture can be found here:
Synopsis:
The global portfolio community accepts Markowitz as the father of the modern portfolio theory.. His work actually completely changed the world of finance. Despite the rapid developments in the field of portfolio construction, the ideas of Modern portfolio theory have become the dominant theory within the investment community. They have inspired many people to develop portfolio selection and management models. Here we develop the logic of portfolio investment based on the same principles, but this time for a multiple-asset portfolio.
Investor’s Space
Between each pair of assets in investors’ space we may draw a concave curve corresponding to the risk-return characteristics of a portfolio constructed with these two assets. Thus, each point in this field will correspond to the risk-return characteristics of a multiple-asset portfolio. Investor space can have various shapes. In this paragraph, however, we shall attempt to prove that the investor or the portfolio manager does not have to outline the whole space in order to select the assets he would like to invest in.
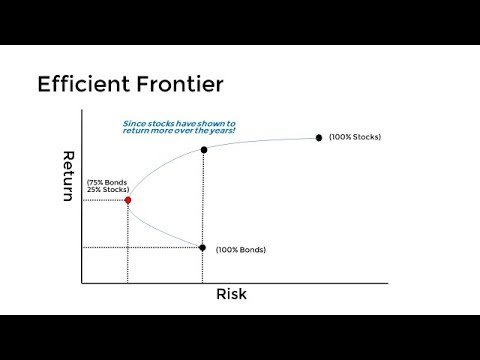
Efficient Frontier
The efficient front is one of the achievements of modern portfolio theory and an indispensable portfolio management tool regardless of the type of model used. It is a curve presenting the portfolios that are the most efficient. Although there are in investor’s space numerous combinations of portfolios that the investor could build, only those portfolios that are positioned as far to the left and as high as possible along the curve are efficient (or reasonable). All other portfolio combinations have worse risk-return characteristics. If the investor is reasonable, he/she will have to select a portfolio positioned along this curve. The curve is of exceptional importance for portfolio theory and practice. The efficient front is the main objective of investors and portfolio managers. Only portfolios along this curve are efficient. This is why we (as reasonable investors) will disregard the inefficient part of the investor field and focus solely on the efficient front.
Utility
The genius of Markowitz concept is that he links the objective and subjective reasons behind investment decisions. If we consider the diversification opportunities separately, we shall see that they can result in an efficient front which exists objectively. Thus, the efficient front defines the best investment opportunities in terms of objective reality. However, the efficient front does not answer the question: Where exactly along the efficient front should we place our investment?
The subjective characteristics of the individual investor may be expressed by the degree of his/her risk-aversion. Each investor has his/her own individual characteristics. This means that his/her level of risk-aversion will depend on his/her individuality and will affect his/her investment decisions. The efficient frontier represents the objective investment opportunities for a given investor. On the other hand, the utility curve represents the investment’s utility function for a certain investor in terms of his/her risk tolerance. Moving the isoquant of curve downwards we arrive at the isoquant which is a tangent to the efficient frontier. The intercept point is simultaneously on the efficient frontier and on the isoquant. Thus, this point combines the subjective and objective reasons for the investment decision, i.e. the efficient portfolio that would provide the best return for the investor-specific level of risk. Therefore, it is the best portfolio investment opportunity which the investor should select. This is the main task of the investor or his/her portfolio manager – to determine that portfolio.
Optimisation
Despite the simplicity of the graphical representation of the model, its mathematical presentation is extremely complex. In order to be as concise as possible, here we shall only describe the formula describing the maximizing the utility function. In fact, it is a risk-return optimisation of the utility function for an individual investor. The first part of equation represents the expected return on the portfolio and the second part, its standard deviation. Therefore, the formula maximises the expected return on the portfolio adjusted by the level of risk taken. The second part of the equation has a negative polarity, which means that the utility will be reduced according to the level of risk associated with the portfolio. The negative polarity means that the investor will try to avoid the risk, i.e. that he/she is risk-averse.
#portfolioptimization #investment #markowitz #mpt #finance #activeinvesting #alpha #efficientfrontier #utility
Synopsis:
The global portfolio community accepts Markowitz as the father of the modern portfolio theory.. His work actually completely changed the world of finance. Despite the rapid developments in the field of portfolio construction, the ideas of Modern portfolio theory have become the dominant theory within the investment community. They have inspired many people to develop portfolio selection and management models. Here we develop the logic of portfolio investment based on the same principles, but this time for a multiple-asset portfolio.
Investor’s Space
Between each pair of assets in investors’ space we may draw a concave curve corresponding to the risk-return characteristics of a portfolio constructed with these two assets. Thus, each point in this field will correspond to the risk-return characteristics of a multiple-asset portfolio. Investor space can have various shapes. In this paragraph, however, we shall attempt to prove that the investor or the portfolio manager does not have to outline the whole space in order to select the assets he would like to invest in.
Efficient Frontier
The efficient front is one of the achievements of modern portfolio theory and an indispensable portfolio management tool regardless of the type of model used. It is a curve presenting the portfolios that are the most efficient. Although there are in investor’s space numerous combinations of portfolios that the investor could build, only those portfolios that are positioned as far to the left and as high as possible along the curve are efficient (or reasonable). All other portfolio combinations have worse risk-return characteristics. If the investor is reasonable, he/she will have to select a portfolio positioned along this curve. The curve is of exceptional importance for portfolio theory and practice. The efficient front is the main objective of investors and portfolio managers. Only portfolios along this curve are efficient. This is why we (as reasonable investors) will disregard the inefficient part of the investor field and focus solely on the efficient front.
Utility
The genius of Markowitz concept is that he links the objective and subjective reasons behind investment decisions. If we consider the diversification opportunities separately, we shall see that they can result in an efficient front which exists objectively. Thus, the efficient front defines the best investment opportunities in terms of objective reality. However, the efficient front does not answer the question: Where exactly along the efficient front should we place our investment?
The subjective characteristics of the individual investor may be expressed by the degree of his/her risk-aversion. Each investor has his/her own individual characteristics. This means that his/her level of risk-aversion will depend on his/her individuality and will affect his/her investment decisions. The efficient frontier represents the objective investment opportunities for a given investor. On the other hand, the utility curve represents the investment’s utility function for a certain investor in terms of his/her risk tolerance. Moving the isoquant of curve downwards we arrive at the isoquant which is a tangent to the efficient frontier. The intercept point is simultaneously on the efficient frontier and on the isoquant. Thus, this point combines the subjective and objective reasons for the investment decision, i.e. the efficient portfolio that would provide the best return for the investor-specific level of risk. Therefore, it is the best portfolio investment opportunity which the investor should select. This is the main task of the investor or his/her portfolio manager – to determine that portfolio.
Optimisation
Despite the simplicity of the graphical representation of the model, its mathematical presentation is extremely complex. In order to be as concise as possible, here we shall only describe the formula describing the maximizing the utility function. In fact, it is a risk-return optimisation of the utility function for an individual investor. The first part of equation represents the expected return on the portfolio and the second part, its standard deviation. Therefore, the formula maximises the expected return on the portfolio adjusted by the level of risk taken. The second part of the equation has a negative polarity, which means that the utility will be reduced according to the level of risk associated with the portfolio. The negative polarity means that the investor will try to avoid the risk, i.e. that he/she is risk-averse.
#portfolioptimization #investment #markowitz #mpt #finance #activeinvesting #alpha #efficientfrontier #utility
 0:11:50
0:11:50
 0:02:54
0:02:54
 0:03:05
0:03:05
 0:01:56
0:01:56
 0:08:47
0:08:47
 0:15:02
0:15:02
 0:21:35
0:21:35
 0:09:12
0:09:12
 0:05:45
0:05:45
 0:03:26
0:03:26
 0:32:47
0:32:47
 0:06:07
0:06:07
 0:35:01
0:35:01
 0:40:21
0:40:21
 0:16:05
0:16:05
 0:09:03
0:09:03
 0:08:21
0:08:21
 0:18:15
0:18:15
 0:08:46
0:08:46
 0:13:48
0:13:48
 1:24:55
1:24:55
 0:10:20
0:10:20
 0:06:36
0:06:36
 1:12:26
1:12:26