Surface Area with a Surface Integral, Multivariable Calculus

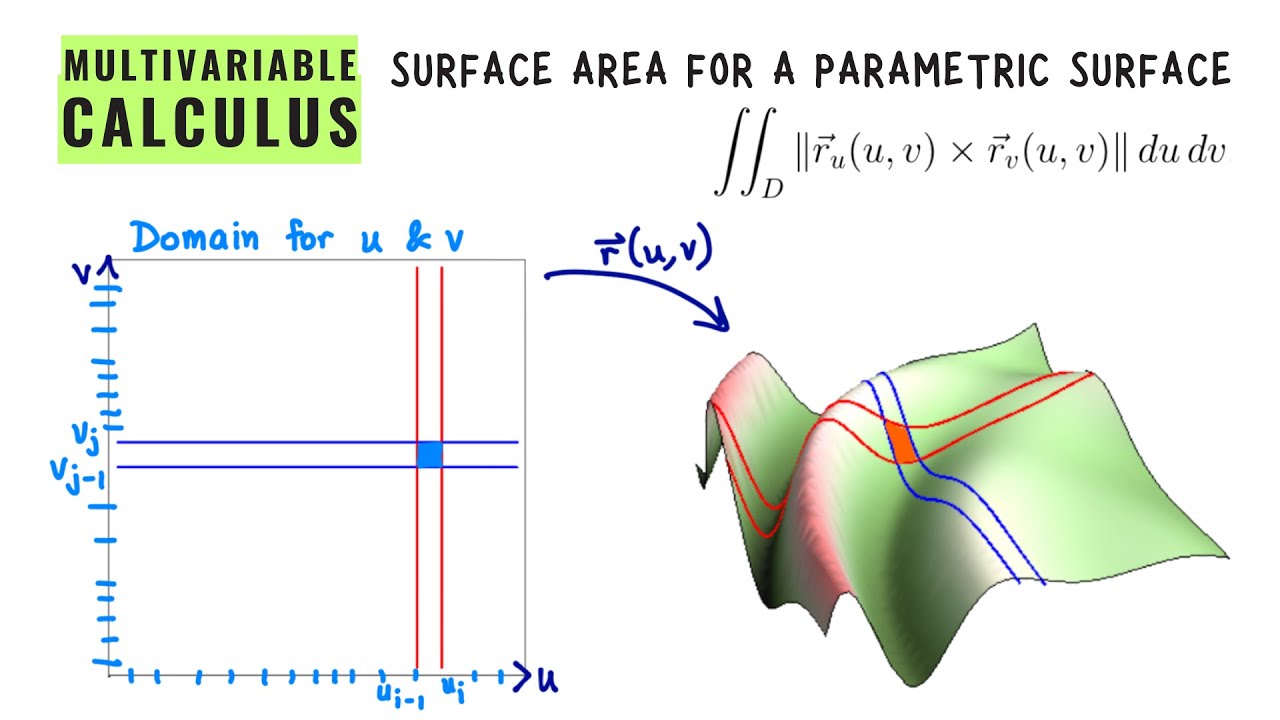
We look at how to use a double integral to compute the surface area of a parametric surface r(u,v). Our derivation will partition the domain of parameters 𝑢 and 𝑣, and map these partitions to approximate parallelograms on the surface. We then utilize cross products to estimate the area of these parallelograms (Unit 1 material!), and through summation and integration, we derive a general formula for surface area. We apply this method to several examples, including the surface area of an upper hemisphere using rectangular, polar, and spherical parametrizations, and the area of a plane section cut by a cylinder. (Unit 6 Lecture 12)

Key Points
- Deriving the formula for the surface area of a parametric surface involves approximating regions on the surface with parallelograms. The area of each parallelogram is estimated using the magnitude of the cross product of vectors corresponding to its sides.
- The results for a parametric surface 𝐫(𝑢,𝑣), (𝑢,𝑣)∈𝐷, is
- Area =∬_𝑆 1 𝑑𝑆 = ∬_𝐷 ‖𝐫𝑢×𝐫𝑣‖ 𝑑𝑢 𝑑𝑣.
- Different parameterizations can simplify the computation, with spherical coordinates often providing the most straightforward integrals for spherical surfaces.

#multivariablecalculus #mathematics #math #surfaceintegral #doubleintegrals #surfaceareaofsolids #surfacearea #iitjammathematics #calculus3