derivative of sin(x) by using the definition of derivative

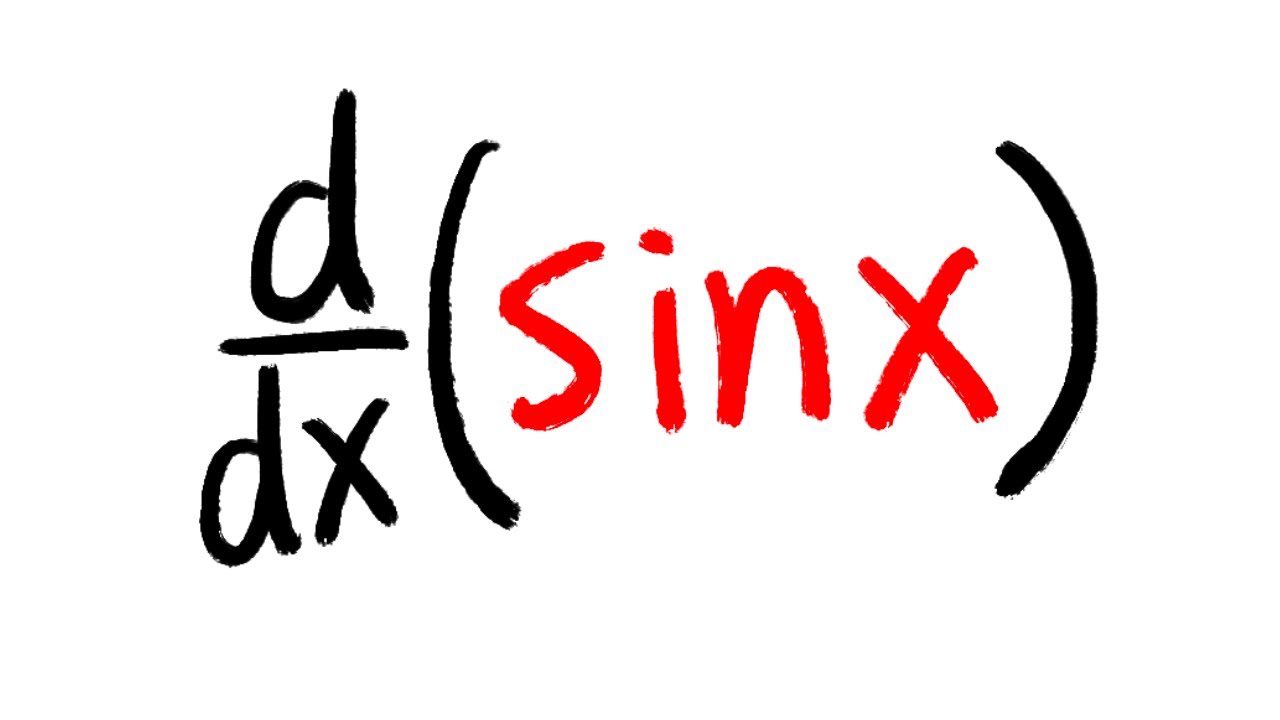
Показать описание

Definition of derivative for sin(x), calculus 1 tutorial. #calculus
----------------------------------------
#blackpenredpen #math #calculus #apcalculus

Рекомендации по теме

Комментарии

"cosh" is tricky, it made me think that it's hyperbollic cosinus for a moment

zygmuntaszczy

I'm not really happy with that omission in the last step. After all, the premise was that we are trying to calculate the derivative of sin(x) as if we were doing it for the first time, and we didn't know what it is. Therefore it feels a bit cheating that then at the end you just assume the result of a limit expression without having to prove it.

DjVortex-w

The last part feels a bit like proof by knowing what the answer is.

ascaniuspotterhead

For question at 6:55,

alternative solution:

d/dx(cos(x))
= d/dx(sin(π/2 - x))
= cos(π/2 - x)(0 - 1)
= -sin(x)

cyrusyeung

TECHNICALLY if you are going to put in 0.0001 h to show it approaches to 1 and zero, you must ALSO put in -0.0001 for h to show it approaches 1 and zero from both sides. Limits approaching from one side isn't always proof of the limit.

peterlohnes

I love how confident you are. Other maths channels constantly add filler. Thanks for the video.

GhostLightPhilosophy

Blackpenredpen, Thanks for your dedication, but in case of when lim(h=0)[(sin(x+h)-sin(x))/h] you could to solve more efficiently by using sum product identity trig formula, derived from two angle manipulation. So, to avoid complicated expression we do sin(x+h)-sin(x)= 2*cos((2x+h)/2)*sin(h/2)). Substituting it, gives us this : lim(h=0)[ 2*cos((2x+h)/2)*sin(h/2))/h], if we rephrase this guy to make appropriate for squeeze theorem (I dont know exactly name, but in my country it calls "first excellent limit" smth like this) => lim(h=0)[ as result we receive following cos(x) because 2 and 2 is deleted from consideration as one of them devide against other, lim(x=0) [sin(x)/x]=1 equivalent to lim(h=0) [sin(h/2)/h/2]=1. Also I wanted to mention that you did not explain the reason of why lim(h=0)[cos(h)-1/h]=0, while such monster expression urgently need detailed explanation with mathematical stunt to understand root of topic. However I love your channel, BEST I HAVE EVER WATCHED [SORRY MAYBE FOR GRAMATICAL MISTAKES, BECAUSE MY LANGUAGE OF INSTRUCTION IS NOT ENGLISH IN MY COUNTRY]

aslankhairashov

There when he states those two limits are 0 and 1, you actually need to use l' Hopital. But that's not fair here, because you need to know the derivative of sinx to do that, which is the very thing you want to prove.

madScientist

Your calculator probably relies on the taylor expansion off the trig functions to calculate them which again relies on the derivate that we are trying to compute in the first place, so it's basically circular reasoning to do it with the calculator

theInternet

From 2:33
Using fundamental theorem of trig
(Sin(small x) = x and cos(small)=1)
We get (sinx+hcosx-sinx)/h = hcosx/h = cosx

canaDavid

After at least 5 years of following this channel I was suggested this video. Now I've learned the proof tha the derivative of sinx is cosx. Thanks.

danielwcrompton

It would be much easier if you considered the limit of (sin(x+h) - sin(x-h))/2h...

cliveso

Thank you so much! I appreciate how you broke down every section step by step, it was very helpful!

NatalieRaphael

in this example approximations work really REALLY well.

sin(h) ~ h for small numbers -> lim sin(h)/h ~ lim h/h = 1

cos(h) ~ 1 for small numbers -> lim (cos(h) -1)/h ~ lim (1-1)/h = 0

EASY

Snwar

This guy is the GOAT. Love the video super informative. Thank you very much!

tobinrose

I wanted this proof.. And you looked smarter in this video than any other one else...

yashkrishnatery

We did it the other way around in school: we defined a function f(x) where f(0)=0, and defined f'(0) to be 1, f''(0)=0, f'''(0)=-1, f''''(0)=0 and so on. Assuming f(x) a polynomial you get a function which is an unlimited sum which approaches sin(x).

Found that fascinating. Not fascinating enough to remember details 25 years later, but still.

karoshi

"They are just like homies"
You crack me up prof! Ty

smoothstriker

Sir
Your teaching method is really different from indian teaching method.

_ashraf.

Let me make something simple for you. People who are asking why is lim of Cos h is 1 and lim of Sine h is 1 ??? It' because when we have the h approaching 0(h is same as theta btw). At that time hypotenuse becomes closer and closer and closer to adjacent side. So Cosine h would be 1. And Sine h would be 1 also.

Sonny

derivative of sin(x) by using the definition of derivative

Proof of the derivative of sin(x) | Derivatives introduction | AP Calculus AB | Khan Academy

derivative of sin(x) by using the definition of derivative

Derivative of sin(x) from First Principles

Derivative of Sine and Cosine Functions | Calculus

Proof of the Derivative of Sinx

Derivative of sin(x) | Animation | mathocube |

Derivative of sin(x) and cos(x), PROOF

Derivative of Sin(x) from first principles

Visualizing the derivative of sin(x)

Derivatives of sin(x) and cos(x) | Derivative rules | AP Calculus AB | Khan Academy

Visual Calculus: Derivative of sin(θ) is cos(θ)

Worked example: Derivatives of sin(x) and cos(x) | Derivative rules | AP Calculus AB | Khan Academy

Differentiating sin(x) from First Principles

A-Level Maths G1-16 Differentiation: Differentiate sin(x) from First Principles

Proof of the derivative of sinx: A Step-by-Step Proof and Explanation

Derivative of sin(x^2), sin^2(x), and sin(2x) with Chain Rule | Calculus 1 Exercises

Find the derivative of y=sinx using the first Principle. find dy/dx w.r.t x

Differentiation - sin(x) and cos(x)

Derivative of Sin(x) using a Graphical approach

Derivative of sin x using First Principle MCV4U

Establishing the Derivatives of sin x, cos x & tan x

Derivative of Sin(x) Proof (Using the Limit Definition)

Derivative of sin(x^2) with Chain Rule | Calculus 1 Exercises

How to use implicit differentiation with trig