filmov
tv
Proof of the derivative of sin(x) | Derivatives introduction | AP Calculus AB | Khan Academy
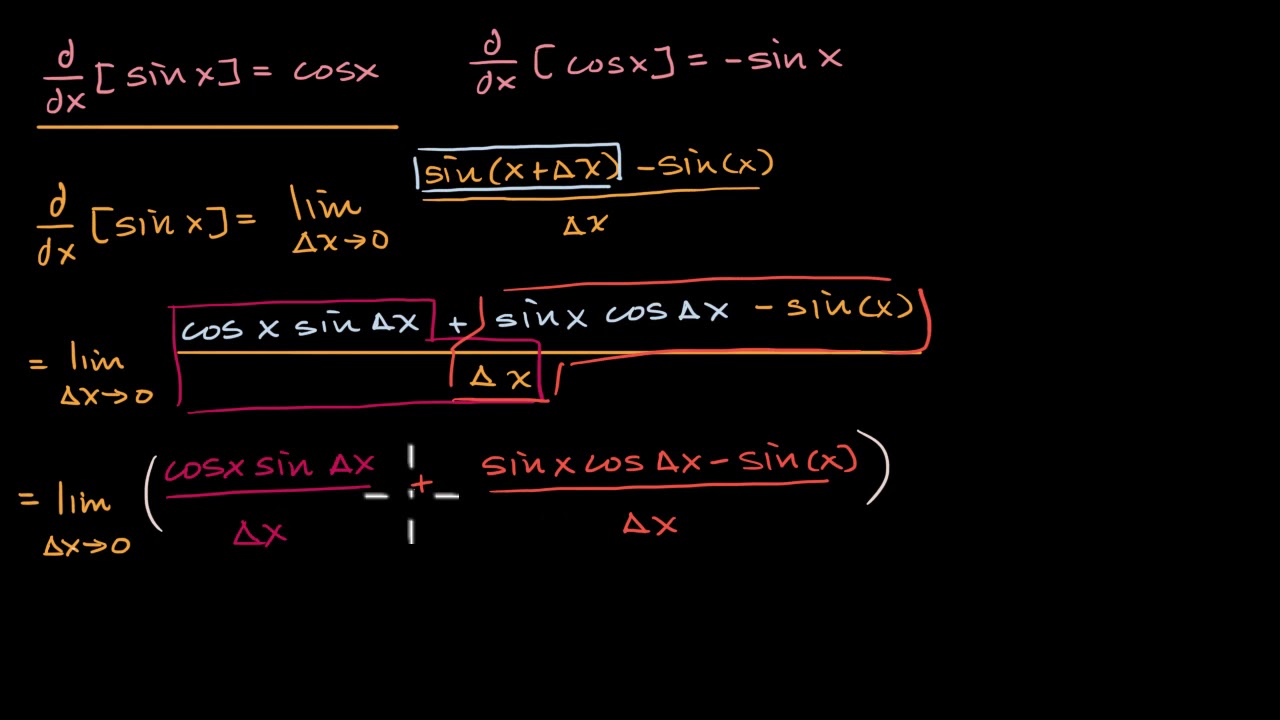
Показать описание
Proving that the derivative of sin(x) is cos(x).
AP Calculus AB on Khan Academy: Bill Scott uses Khan Academy to teach AP Calculus at Phillips Academy in Andover, Massachusetts, and he’s part of the teaching team that helped develop Khan Academy’s AP lessons. Phillips Academy was one of the first schools to teach AP nearly 60 years ago.
For free. For everyone. Forever. #YouCanLearnAnything
Proof of the derivative of sin(x) | Derivatives introduction | AP Calculus AB | Khan Academy
Proof of the derivative of e^x: A Step-by-Step Proof and Explanation
Proof: The derivative of __ is __ | Advanced derivatives | AP Calculus AB | Khan Academy
Proofs of derivatives of ln(x) and e^x | Taking derivatives | Differential Calculus | Khan Academy
Proof of the derivative of cos(x) | Derivative rules | AP Calculus AB | Khan Academy
Proof of the Formula for the Derivative of a^x
Chain rule proof | Derivative rules | AP Calculus AB | Khan Academy
Derivative as a concept | Derivatives introduction | AP Calculus AB | Khan Academy
Uniqueness Theorem: Basics, Derivation, and Proof
Proof: the derivative of ln(x) is 1/x | Advanced derivatives | AP Calculus AB | Khan Academy
Proof of the derivative of cosx: A Step-by-Step Proof and Explanation
Induction: Derivative Proof
Definition of the Derivative
Visual Derivative Definition!
Proof: Derivative of ln(x) = 1/x by First Principles
Proof of the Derivative of the Exponential Functions
Proof of the derivative of sinx: A Step-by-Step Proof and Explanation
Proof: Derivative of Constant
Proof of the derivative of tanx: A Step-by-Step Proof and Explanation
Proof of the Derivative of Sinx
Visual Calculus: Derivative of sin(θ) is cos(θ)
My friend showed me 1=2 proof by using derivative and I am kind of stumped. Reddit r/calculus
Proof: Derivative of e^x is e^x
Derivative from First Principles
Комментарии
 0:05:52
0:05:52
 0:03:51
0:03:51
 0:08:39
0:08:39
 0:12:27
0:12:27
 0:03:18
0:03:18
 0:03:01
0:03:01
 0:05:39
0:05:39
 0:07:16
0:07:16
 0:09:14
0:09:14
 0:08:08
0:08:08
 0:04:53
0:04:53
 0:11:30
0:11:30
 0:23:31
0:23:31
 0:01:00
0:01:00
 0:08:14
0:08:14
 0:02:35
0:02:35
 0:06:06
0:06:06
 0:02:39
0:02:39
 0:06:09
0:06:09
 0:04:57
0:04:57
 0:03:08
0:03:08
 0:04:48
0:04:48
 0:10:24
0:10:24
 0:07:35
0:07:35