Derivative of sin(x) and cos(x), PROOF

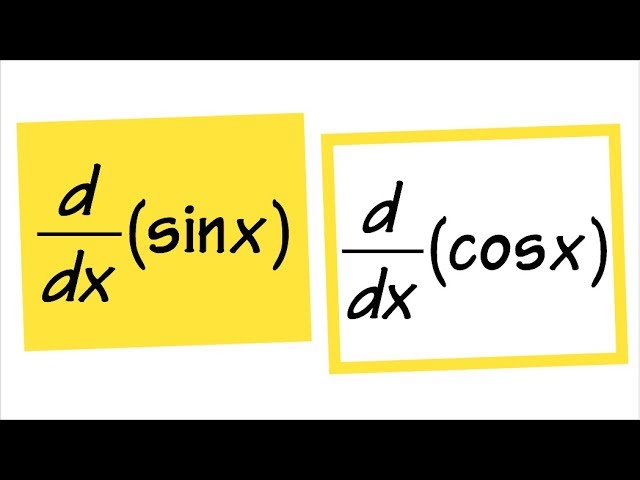
Показать описание

Please subscribe and share my videos to help my channel grow! 😃

Comment #YAY down below & your comment might be featured in my future videos!!!

Check out my site & social media

Thank you for watching!
blackpenredpen | 曹老師

Рекомендации по теме

Комментарии

I saw a student using L'Hospital for this, it made me really angry because he used sin'(x) to calculate sin'(x)

PackSciences

"sine and cosine are like homies" #yay

alexdarcovich

Prefect! I didn't know that cosine stands for complement of sine. Thanks for the video!

JuditaKindlova

Student: I'm so smart, I know how to derive all the trig function derivatives
Bprp: Really? Can you show me it for sin and cos then
Student: ...
#yay

darnellyiadom

You can also use the identity sin^2 + cos^2 = 1 and derive both sides then you got (sin^2 + cos^2) ‘ = 0 and (cos^2) ‘ = -(sin^2)’ so 2cos*(cos)’ = -2sincos and so (cos)’ = -sin

Engeneeringtips

Can u do that proof of cosh-1/h and sinh/h

rishisivakumar

I ended with lim as h->0 cos(x)*sin(h/2)/(h/2). Using some tricks with the e^iz formula xD.

hc_

In summary, It's like 19÷4 = 19/4

HamedAbdulla

Master Cao, no explanation of why (cos(h)-1)/h tend to 0 when h tend to 0

gagadaddy

Nice! I hadn't thought about using complementary identity to prove the derivative of cos(x)

alejrandom

Thanks a lot sir .
Amazing explaintion 😀

redone

God bless you instead lecture was superb 👏🏻👏🏻

Alisha-lxir

Why not do the derivative based on the Maclaurin series for since and cosine? The approach you used here has the issue that, without the numerical ✋ waving you might have been stuck with L'Hospital's rule, essentially needing to know the answer to the derivative you were trying to find.

Maybe there's a non-circular, rigorous way to solve the "0/0" limits without L'Hospital's rule, but it didn't come readily to mind.

ckmishn

Since we're all adults now... Tee-hee! 😁

banderfargoyl

2:05 for those ho want to understand how he get the rule; go watch videos about addition and soustraction for cosinus and sinus cos(a+b) cos(a-b) sinus (a+b) sinus (a-b) it s kinda difficult but you will understand it ; then after that get back to the video

levi

A more elegant and compact proof exists which uses the identity SinC - SinD = 2Sin(C-D)/2*Cos(C+D)/2 together with the limit Sinh/h ➡️ 1 as h ➡️ 0.

Note, C = (x + h) and D = x.
Substitution: lim h ➡️ 0 (2Sinh/2h)*(Cos((2x+h)/2)) evaluates to (1)*(Cos(2x/2)) which, in turn, evaluates to Cosx.

FFFGP

I figured out two proofs that don’t use the limit of sin x/x, the limit of (cos x–1)/x, or any angle-sum identity. One uses the definition of arc length (as well as the Pythagorean theorem, the fundamental theorem of calculus, and the derivative of sqrt(1–x^2)), but the other one just uses the parametric definition of a derivative (d[x, y]/dt=[dx/dt, dy/dt]). If I ever teach a math class, I will be looking for one of those.

jackkalver

Can you prove
tan(x+y) = BTW thanks so much, I learned much in your videos.

joshuapaulorigenes

This is really neat! Glad I found this! =D

MrLuigiBean

You can also use the expansion of sinx and it is very easy with that approch

ankursrivastava

Derivative of sin(x) and cos(x), PROOF

Derivative of Sine and Cosine Functions | Calculus

Derivative of sin(x) and cos(x), PROOF

Differentiation - sin(x) and cos(x)

Derivatives of sin(x) and cos(x) | Derivative rules | AP Calculus AB | Khan Academy

Worked example: Derivatives of sin(x) and cos(x) | Derivative rules | AP Calculus AB | Khan Academy

Derivative of sin(x) and cos(x)

Proof of the derivative of sin(x) | Derivatives introduction | AP Calculus AB | Khan Academy

Establishing the Derivatives of sin x, cos x & tan x

JEE 2nd way If y=log(sin(x degree)+cos(x degree)), find dy/dx

Derivative of sinxcosx with Product Rule | Calculus 1 Exercises

Derivatives of sin x, cos x, tan x, e^x and ln x

Derivative of sinx/cosx with Quotient Rule | Calculus 1 Exercises

Visual Calculus: Derivative of sin(θ) is cos(θ)

Calculus Product Rule Example f(x) = sin(x)*cos(x)

How to find the Derivative of sin(x), cos(x) and tan(x)

Differentiating sin x and cos x from first principles

Edexcel A level Maths: 9.1 First Principles, Differentiating Sin(x) and Cos(x)

Calculus AB/BC – 2.7 Derivatives of cos(x), sin(x), e^x, and ln(x)

Derivative of Sine X = Cos X || Differentiate Sin X || Proof in Calculus Math

Differentiating sin(x), cos(x) and tan(x)

Taylor series for sin(x) and cos(x), Single Variable Calculus

Proof: Derivative of Sin is Cos (Version 2)

Proof of the derivative of cos(x) | Derivative rules | AP Calculus AB | Khan Academy

Derivative of Cos x from First Principles.