filmov
tv
An Infinite Radical Expression | The Golden Ratio

Показать описание
🤩 Hello everyone, I'm very excited to bring you a new channel (SyberMath Shorts).
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #Radicals
via @YouTube @Apple @Desmos @NotabilityApp
@googledocs @canva
SIMILAR PROBLEMS 🤩
PLAYLISTS 🎵 :
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #Radicals
via @YouTube @Apple @Desmos @NotabilityApp
@googledocs @canva
SIMILAR PROBLEMS 🤩
PLAYLISTS 🎵 :
An Infinite Radical Expression!!!
Simplifying An Infinite Radical Expression
An Infinite Radical Expression
Simplifying An Infinite Radical Expression
An Infinite Radical Equation
An Infinite Radical Expression
An Infinite Radical Expression
An Infinite Radical Solved in Two Ways
Root Simplification Tricks You Wish You Knew #shorts
An Infinite Radical Expression | Shorts
A nice infinite radical problem
An Infinite Radical Expression... | Math Olympiads
How to simplify an infinite radical expression |@goymath
Infinite Nested Radical
An Infinite Radical Expression | The Golden Ratio
Simplifying an Infinite Radical
A Nice Infinite Radical
Simplifying A Nice Radical Expression
An Infinite Radical | Algebra Challenge
Simplifying an Infinite Radical | My First Short
Infinite Radical Equation | Daily Math Algebra
An Infinite Radical with A Golden Flavor
An Infinite Radical with a Variable
An Infinite Radical Equation | Problem 417
Комментарии
 0:02:00
0:02:00
 0:08:48
0:08:48
 0:00:40
0:00:40
 0:08:48
0:08:48
 0:04:29
0:04:29
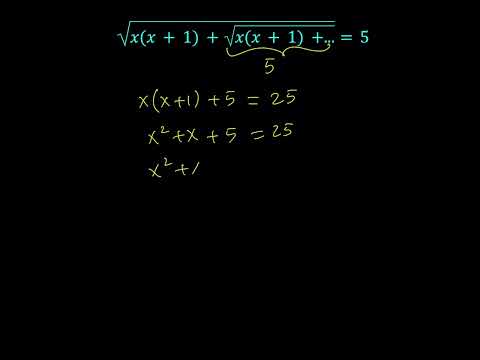 0:00:40
0:00:40
 0:00:29
0:00:29
 0:08:48
0:08:48
 0:00:34
0:00:34
 0:00:29
0:00:29
 0:03:35
0:03:35
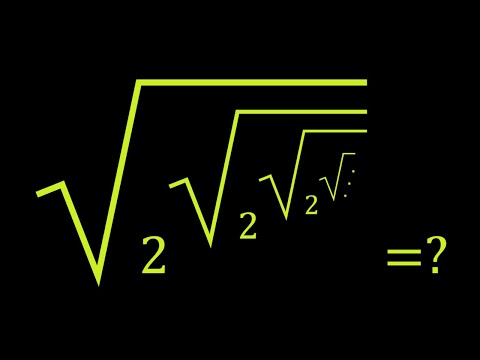 0:11:11
0:11:11
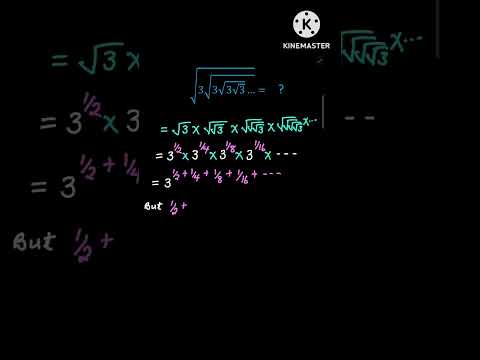 0:00:28
0:00:28
 0:03:55
0:03:55
 0:09:33
0:09:33
 0:00:45
0:00:45
 0:02:59
0:02:59
 0:00:39
0:00:39
 0:00:39
0:00:39
 0:00:45
0:00:45
 0:03:38
0:03:38
 0:00:41
0:00:41
 0:00:58
0:00:58
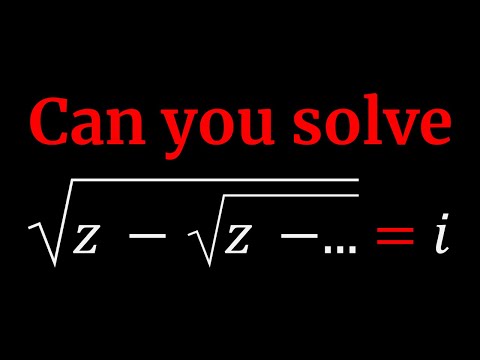 0:08:25
0:08:25