filmov
tv
Vertical Asymptotes... How? (NancyPi)

Показать описание
MIT grad shows how to find the vertical asymptotes of a rational function and what they look like on a graph. To skip ahead: 1) For the STEPS TO FIND THE VERTICAL ASYMPTOTE(S) and an example with two vertical asymptotes, skip to 0:19. 2) For an example in which FACTORS CANCEL and that has one vertical asymptote and a HOLE, skip to 5:58. 3) For an example with NO VERTICAL ASYMPTOTES, skip to time 10:12. Nancy formerly of MathBFF explains the steps.
What is a vertical asymptote? It's an invisible vertical line that a function gets really really close to but never reaches. How do you find the vertical asymptote(s) from the given equation?
THREE STEPS TO FIND THE VERTICAL ASYMPTOTE(S): For a rational function, there are three main steps you can always follow to find all the vertical asymptotes, if there are any:
STEP 1) FACTOR: The first step is to factor the top and bottom (numerator and denominator) if you can, and as much as you can. For instance, in the function f(x) = (x^2 + 3x - 10)/(x^2 - 4), you can factor both the top and bottom. The numerator, x^2 + 3x - 10, is a quadratic that factors into (x + 5)(x - 2), and the denominator, x^2 - 4, is a difference of squares that factors into (x + 2)(x - 2). You then rewrite the whole function with both of these factorizations so that you have f(x) = [(x + 5)(x - 2)] / [(x + 2)(x - 2)].
STEP 2) CANCEL: Next, simplify the function by canceling any factors that are the same on top and bottom. If there are no common factors, you can leave it alone. In our example from Step 1, there is an x - 2 term on both the top and bottom, so we can cancel those two factors. You can rewrite the function after getting rid of those similar factors so that it looks like: f(x) = (x + 5)/(x + 2).
STEP 3) SET THE DENOMINATOR EQUAL TO ZERO: After simplifying and getting rid of any common factors, the last step is to find the real zeros of the denominator by taking the bottom of the simplified function and setting it equal to zero. You then solve that equation for x, and any real numbers you get as a solution for x are where there are vertical asymptotes. You can write your answers as just "x equals [some number]". If you have vertical asymptotes, they will always be in that form, such as x = 3 or x = -2. These represent vertical (invisible) lines on the graph that your function approaches but never crosses.
Remember that if you get an imaginary answer when you solve for x (such as a square root of a negative number), then there are no vertical asymptotes. If there is no real solution when you solve for x, then there are NO VERTICAL ASYMPTOTES. Note: By the way, if you had factors that cancelled in Step 2, that created a "hole", or removable discontinuity, on the graph where the function was indeterminate.
What is a vertical asymptote? It's an invisible vertical line that a function gets really really close to but never reaches. How do you find the vertical asymptote(s) from the given equation?
THREE STEPS TO FIND THE VERTICAL ASYMPTOTE(S): For a rational function, there are three main steps you can always follow to find all the vertical asymptotes, if there are any:
STEP 1) FACTOR: The first step is to factor the top and bottom (numerator and denominator) if you can, and as much as you can. For instance, in the function f(x) = (x^2 + 3x - 10)/(x^2 - 4), you can factor both the top and bottom. The numerator, x^2 + 3x - 10, is a quadratic that factors into (x + 5)(x - 2), and the denominator, x^2 - 4, is a difference of squares that factors into (x + 2)(x - 2). You then rewrite the whole function with both of these factorizations so that you have f(x) = [(x + 5)(x - 2)] / [(x + 2)(x - 2)].
STEP 2) CANCEL: Next, simplify the function by canceling any factors that are the same on top and bottom. If there are no common factors, you can leave it alone. In our example from Step 1, there is an x - 2 term on both the top and bottom, so we can cancel those two factors. You can rewrite the function after getting rid of those similar factors so that it looks like: f(x) = (x + 5)/(x + 2).
STEP 3) SET THE DENOMINATOR EQUAL TO ZERO: After simplifying and getting rid of any common factors, the last step is to find the real zeros of the denominator by taking the bottom of the simplified function and setting it equal to zero. You then solve that equation for x, and any real numbers you get as a solution for x are where there are vertical asymptotes. You can write your answers as just "x equals [some number]". If you have vertical asymptotes, they will always be in that form, such as x = 3 or x = -2. These represent vertical (invisible) lines on the graph that your function approaches but never crosses.
Remember that if you get an imaginary answer when you solve for x (such as a square root of a negative number), then there are no vertical asymptotes. If there is no real solution when you solve for x, then there are NO VERTICAL ASYMPTOTES. Note: By the way, if you had factors that cancelled in Step 2, that created a "hole", or removable discontinuity, on the graph where the function was indeterminate.
Комментарии
 0:13:01
0:13:01
 0:04:42
0:04:42
 0:00:59
0:00:59
 0:10:54
0:10:54
 0:08:42
0:08:42
 0:01:15
0:01:15
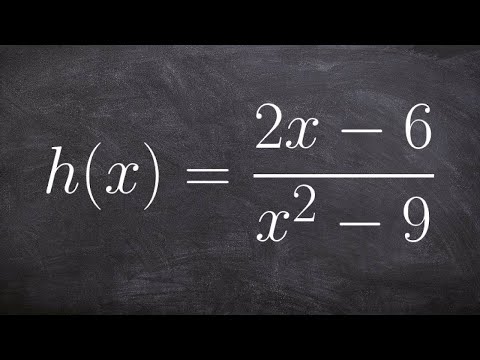 0:02:16
0:02:16
 0:01:18
0:01:18
 0:05:14
0:05:14
 0:00:14
0:00:14
 0:40:21
0:40:21
 0:05:33
0:05:33
 0:08:53
0:08:53
 0:27:57
0:27:57
 0:03:08
0:03:08
 0:30:24
0:30:24
 0:00:06
0:00:06
 0:00:21
0:00:21
 0:06:40
0:06:40
 0:03:51
0:03:51
 0:00:31
0:00:31
 0:07:24
0:07:24
 0:08:02
0:08:02
 0:07:05
0:07:05