filmov
tv
\[ \begin{array}{l} \text { Comprehension } \\ \text { trigonometric functions be defined } \qua...

Показать описание
\[
\begin{array}{l}
\text { Comprehension } \\
\text { trigonometric functions be defined } \quad \begin{array}{l}
\text { Let } \\
\text { as }
\end{array} \\
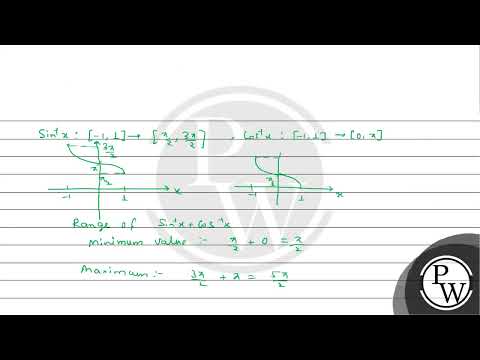
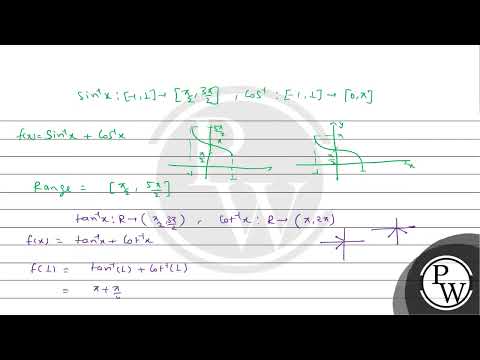
\sin ^{-1} x:[-1,1] \rightarrow\left[\frac{\pi}{2}, \frac{3 \pi}{2}\right] ; \quad \cos ^{-1} \quad x:[-1,1] \rightarrow[0, \pi] \\
\tan ^{-1} x: R \rightarrow\left(\frac{\pi}{2}, \frac{3 \pi}{2}\right) ; \cot ^{-1} x: R \rightarrow(\pi, 2 \pi) ; \\
\operatorname{cosec}^{-1} x:(-\infty,-1] \cup[1, \infty) \rightarrow\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]-\{0\} ; \\
\sec ^{-1} x:(-\infty,-1] \cup[1, \infty) \rightarrow[0, \pi]-\left\{\frac{\pi}{2}\right\} .
\end{array}
\]
Match maximum value of expression in Column-I and minimum value of expression in Column-II to corresponding values given in Column-III.
\begin{tabular}{|r|l|r|l|l|c|}
\hline \multicolumn{2}{|c|}{ Column-I } & \multicolumn{2}{c|}{ Column-II } & \multicolumn{2}{c|}{ Column-III } \\
\hline I. & \( \sin ^{-1} x+\cos ^{-1} x \) & i. & \( \tan ^{-1} x+\cot ^{-1} x \) & P. & 0 \\
\hline II. & \( \sin ^{-1}(-x)+\sin ^{-1} x \) & ii. & \( \tan ^{-1} x+\tan ^{-1}(-x) \) & Q. & \( \frac{\pi}{2} \) \\
\hline III. & \( \cot ^{-1} x+\cot ^{-1}(-x)-\frac{5 \pi}{2} \) & iii. & \( \sec ^{-1}\left(\frac{1}{x}\right)+\cos ^{-1}(x) \) & R. & \( 2 \pi \) \\
\hline IV. & \( \operatorname{cosec}^{-1}\left(\frac{1}{x}\right)+\sin ^{-1} x-\pi \) & iv. & \( \sec ^{-1} x+\operatorname{cosec}^{-1} x \) & S. & \( \frac{5 \pi}{2} \) \\
\hline
\end{tabular}
Which of the following combination is correct?
(a) (I) (i) (P)
(b) (I) (ii) (R)
\( (c)(\mathrm{I})(\mathrm{i})(\mathrm{S}) \)
(d) (II) (i) ( R)
\begin{array}{l}
\text { Comprehension } \\
\text { trigonometric functions be defined } \quad \begin{array}{l}
\text { Let } \\
\text { as }
\end{array} \\
\sin ^{-1} x:[-1,1] \rightarrow\left[\frac{\pi}{2}, \frac{3 \pi}{2}\right] ; \quad \cos ^{-1} \quad x:[-1,1] \rightarrow[0, \pi] \\
\tan ^{-1} x: R \rightarrow\left(\frac{\pi}{2}, \frac{3 \pi}{2}\right) ; \cot ^{-1} x: R \rightarrow(\pi, 2 \pi) ; \\
\operatorname{cosec}^{-1} x:(-\infty,-1] \cup[1, \infty) \rightarrow\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]-\{0\} ; \\
\sec ^{-1} x:(-\infty,-1] \cup[1, \infty) \rightarrow[0, \pi]-\left\{\frac{\pi}{2}\right\} .
\end{array}
\]
Match maximum value of expression in Column-I and minimum value of expression in Column-II to corresponding values given in Column-III.
\begin{tabular}{|r|l|r|l|l|c|}
\hline \multicolumn{2}{|c|}{ Column-I } & \multicolumn{2}{c|}{ Column-II } & \multicolumn{2}{c|}{ Column-III } \\
\hline I. & \( \sin ^{-1} x+\cos ^{-1} x \) & i. & \( \tan ^{-1} x+\cot ^{-1} x \) & P. & 0 \\
\hline II. & \( \sin ^{-1}(-x)+\sin ^{-1} x \) & ii. & \( \tan ^{-1} x+\tan ^{-1}(-x) \) & Q. & \( \frac{\pi}{2} \) \\
\hline III. & \( \cot ^{-1} x+\cot ^{-1}(-x)-\frac{5 \pi}{2} \) & iii. & \( \sec ^{-1}\left(\frac{1}{x}\right)+\cos ^{-1}(x) \) & R. & \( 2 \pi \) \\
\hline IV. & \( \operatorname{cosec}^{-1}\left(\frac{1}{x}\right)+\sin ^{-1} x-\pi \) & iv. & \( \sec ^{-1} x+\operatorname{cosec}^{-1} x \) & S. & \( \frac{5 \pi}{2} \) \\
\hline
\end{tabular}
Which of the following combination is correct?
(a) (I) (i) (P)
(b) (I) (ii) (R)
\( (c)(\mathrm{I})(\mathrm{i})(\mathrm{S}) \)
(d) (II) (i) ( R)
 0:09:25
0:09:25
 0:09:43
0:09:43
 0:14:15
0:14:15
 0:10:51
0:10:51
 0:02:12
0:02:12
 0:04:16
0:04:16
 0:04:21
0:04:21
 0:13:40
0:13:40
 0:08:27
0:08:27
 0:07:55
0:07:55
 0:02:27
0:02:27
 0:14:51
0:14:51
 4:22:13
4:22:13
 0:01:41
0:01:41
 0:03:09
0:03:09
 0:02:42
0:02:42
 0:04:41
0:04:41
 0:11:25
0:11:25
 0:11:32
0:11:32
 0:04:59
0:04:59
 0:11:40
0:11:40
 0:05:50
0:05:50
 0:00:58
0:00:58
 0:13:02
0:13:02