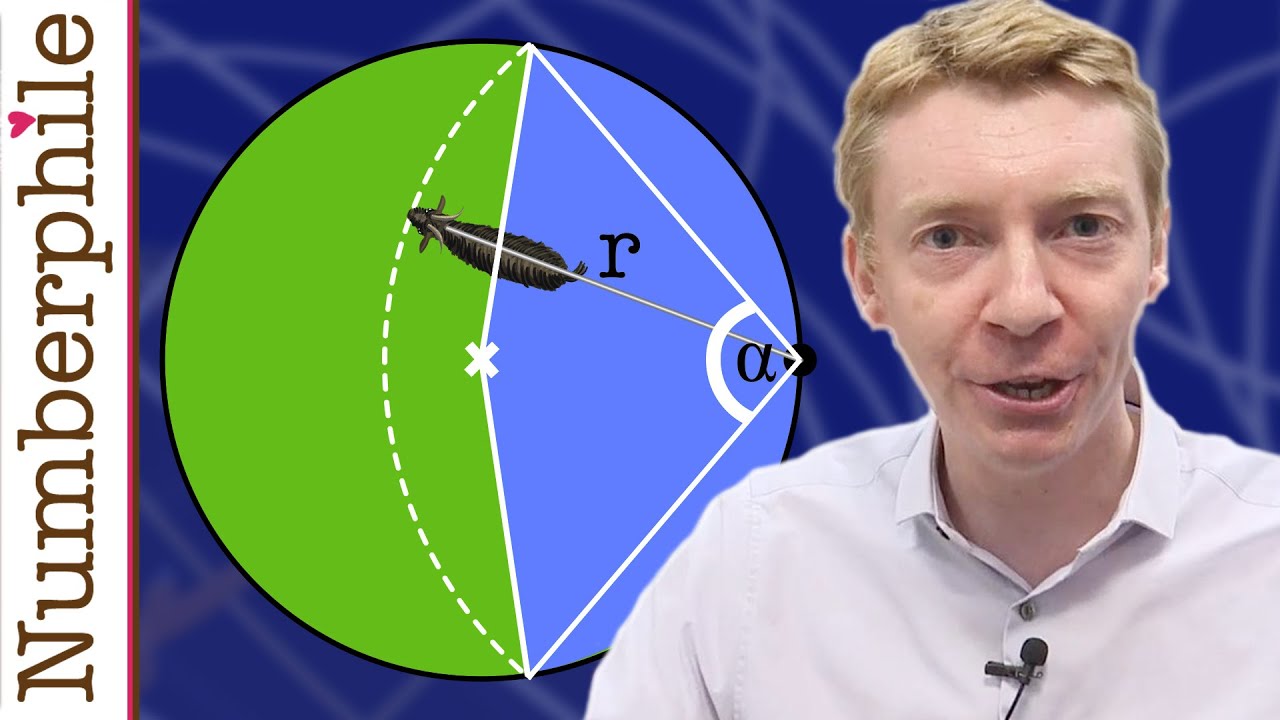
The Goat Problem - Numberphile

More links & stuff in full description below ↓↓↓

Some papers about the Goat Problem...

NUMBERPHILE

Videos by Brady Haran
Animation by Pete McPartlan
With thanks to our checkers, including János Pallagi

[counting]

I love Dr Grime . His smile is infectious and it just makes me excited to learn more .

[willk]

The complex number version only works with imaginary goats.

[stuartcoyle]

I've owned goats. I know the answer: the goat will jump the fence, chew through the rope, pull the fence down, eat anything but the grass, escape and cause chaos in the neighbour's yard.

[ffs]

I love how mathematicians casually talk about goats grazing in 5 dimensions whilst frowning upon tangible real-world numerical answers...

[davidgillies]

Couple of friends of mine wrote a paper years ago on a generalisation of this problem and its connection to optimal siting of a radar jammer, or nodes in a mesh network to avoid mutual interference. It was called "On Goats and Jammers" and the technique used there was to split the problem into two integrals, one for the real part of the problem and one for the imaginary part (Shepherd and van Eetvelt, Bulletin of the IMA, May 95). The abstract says "The technique is a generalisation of the classical “goat eating a circular field” problem, which is resolved in passing".

[koenth]

For those interested in the trig:

1) Area of arc part (swept by tight tether)
A1 = r^2 α/2 = 2α cos^2(α/2) = α (1+ cos(α))

2) Area (swept by circle radius over the part of the circle that goat can visit)
A2 = π-α

3) Overlap (four equal right-angled triangles)
A3 = 2cos(α/2)sin(α/2) = sin(α)

So we have to solve A1 + A2 - A3 = π/2, or  α (1+ cos(α)) + π-α - sin(α) = π/2 which simplifies to

α cos(α) - sin(α) + π/2 = 0

This gives
α ≈ 1.90569572930988... (radians)
r  ≈ 1.15872847301812...

[matematicaspanish]

James Grime being friends with Graham Jameson is almost as impressive as the goat situation

[farzaan]

15:35 it actually is an important problem! I had to use it for my research in biology! Basically it was to calculate how the effusion of a substance in a circular arena affects animals and I stumbled across it online when I realized how difficult it was to calculate by hand, really great stuff!

[PotatoMcWhiskey]

I think Grimes is one of the best people featured on this channel
Every video is a joy to watch

[Axacqk]

This will probably be said later in the video, but it just dawned on me that r tends to sqrt(2) in high dimensions because the volume of high-dimensional hyperballs is increasingly concentrated near the surface (a fact I probably learned from another Numberphile video), and r=sqrt(2) always halves the surface exactly.

[lasagnahog]

There are very few people I've been watching on youtube longer than Dr. Grime. It's always a treat to see him pop up here.

[DanDart]

I was taught this problem at school, and I think I recall that I was told that it was solvable exactly using only secondary school maths we had already learned. We spent the entire lesson trying to work it out, and it's not left my mind for half my life.

[EaglePL]

That practice explanation at the end is so important, people always complain about money being spent on research that yields nothing or random seemingly useless knowledge but the researchers have to learn, improve process and tools somehow. Satisfying curiosity is important to help people focus, also tiny findings may help someone else with their process in the future.

[jonathanlister]

An actual Goat would simply chew through its tether as it's not limited by mathematics.

[Bibibosh]

James Grime is one of my most favorite personalities on Numberphile. You guys really feel like a friend :D and I would definitely recognize you guys in public!

[fmaz]

So, the new challenge is to solve it in 1 dimension.

[autumn_skies]

I always love seeing Dr. Grime on this channel! ❤️

[chloelo]

Been following Dr. Grime on Numberphile for years and it’s always a delight to see his enthusiasm. I’ve been away from recreational maths because full time job gets in the way, but this video reminds me of those puzzle cracking days, which were awesome. And it’s also really really nice to see Dr Grime not changing a bit in his passion talking about maths in an accessible way to the general public.

[vlastasusak]

All we need to do is construct a collapsible Peaucellier-Lipkin linkage and tether the goat to that. Then the boundry of it's constraint will be a straight line instead of an arc, and figuring out the necessary length will be easy

[trdi]

That's impressive. I don't understand the question "Why did he do that?" Why wouldn't he do it? It's cool.