filmov
tv
The Monty Hall Problem: Switch Doors or Not?
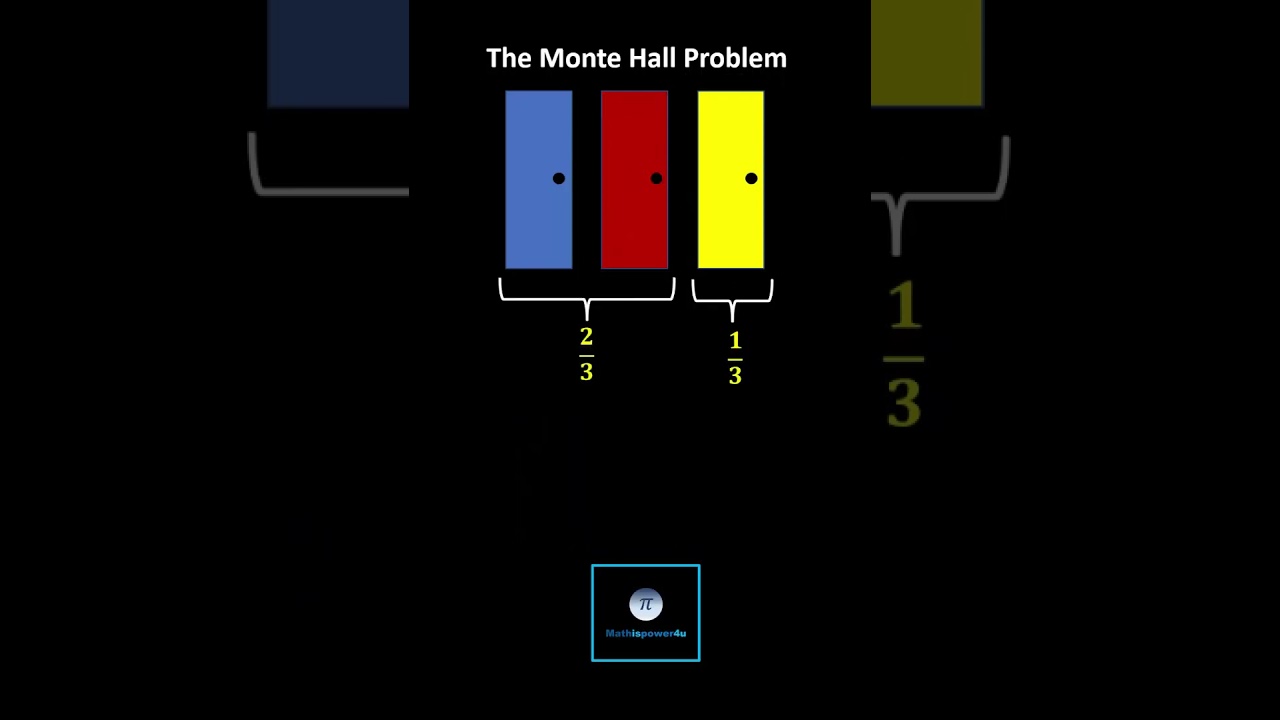
Показать описание
#shorts This video presents a problem related to the famous Monty Hall Problem. You may also like this longer explanation that considers more the 3 doors.
The Monty Hall Problem - Explained
The Monty Hall Problem: Switch Doors or Not?
Monty Hall Problem Express Explanation
The Monty Hall Problem - Why Switching Is Better ('I Finally Understand It')
Monty Hall Problem - Numberphile
The Monty Hall Problem: Switch Doors or Stay?
The Monty Hall Problem
Monty Hall Problem (best explanation) - Numberphile
The Monty Hall Problem | Brooklyn Nine-Nine
The Monty Hall Problem: Switch Doors or Not?
The math problem that stumped thousands of mansplainers
Monty Hall Problem explained (3 doors, n doors)
Monty Hall Problem (extended math version)
Proving The Monty Hall Problem
The Monty Hall Problem Explained
The Monty Hall Problem
The Monty Hall Problem
The Monty Hall Problem 😨 (explained)
Coding Challenge 170: The Monty Hall Problem
Monty Hall II: Revenge of Monty Hall
The Monty Hall Problem : Why You Should Always Switch
Let’s Rethink the Monty Hall Problem
The Monty Hall Problem - Math Mark
21 - Monty Hall - PROPENSITY BASED THEORETICAL MODEL PROBABILITY - MATHEMATICS in the MOVIES
Комментарии
 0:02:48
0:02:48
 0:00:50
0:00:50
 0:00:49
0:00:49
 0:02:16
0:02:16
 0:05:30
0:05:30
 0:02:18
0:02:18
 0:14:01
0:14:01
 0:04:18
0:04:18
 0:03:37
0:03:37
 0:04:15
0:04:15
 0:04:58
0:04:58
 0:09:24
0:09:24
 0:10:14
0:10:14
 0:03:33
0:03:33
 0:07:02
0:07:02
 0:15:59
0:15:59
 0:01:45
0:01:45
 0:01:00
0:01:00
 0:32:16
0:32:16
 0:03:55
0:03:55
 0:03:44
0:03:44
 0:01:00
0:01:00
 0:10:03
0:10:03
 0:03:04
0:03:04