filmov
tv
A Problem with the Parallel Postulate - Numberphile

Показать описание
Featuring Juanita Pinzón Caicedo from University of Notre Dame.
More links & stuff in full description below ↓↓↓
NUMBERPHILE
Videos by Brady Haran
More links & stuff in full description below ↓↓↓
NUMBERPHILE
Videos by Brady Haran
A Problem with the Parallel Postulate - Numberphile
Gr 9 Geometry: Parallel lines
CppCon 2014: Pablo Halpern 'Decomposing a Problem for Parallel Execution'
How to Solve Any Series and Parallel Circuit Problem
GCSE Maths - Alternate, Corresponding and Allied Angles - Parallel Lines Angle Rules #117
Are Parallel Societies a Problem? : Dr. Elham Manea at TEDxBern
Finding Missing Angles, Parallel Lines and Transversal Ex.
AS Maths - Pure - Parallel Lines
PARALLEL LIVES IN THE PHILIPPINES...DONT FORGET 🤔 loop
Issue with Parallel Streams in Java8 | What is Java Parallel Streams| When to use Parallel Stream
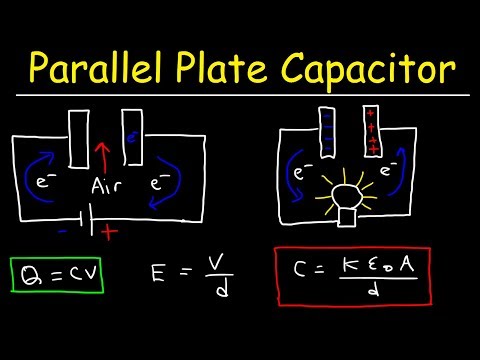
Parallel Plate Capacitor Physics Problems
A-Level Maths: S1-25 Non-Parallel Forces: An Introduction to Ladders
How To Solve Any Resistors In Series and Parallel Combination Circuit Problems in Physics
Solving Problems involving PARALLEL LINES CUT BY A TRANSVERSAL | Ms Rosette
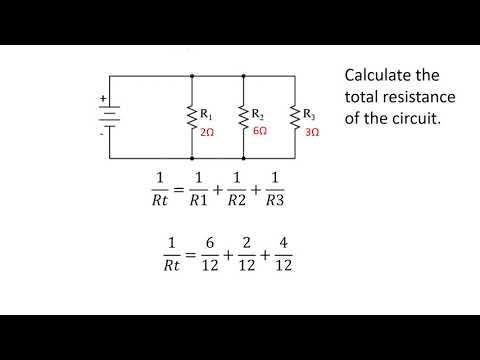
Calculating resistance in parallel
How To Solve Any Circuit Problem With Capacitors In Series and Parallel Combinations - Physics
Problem Set #3 - Intro to Parallel Programming
Art of Problem Solving: Angles and Parallel Lines
Parallel Axis Theorem & Moment of Inertia - Physics Practice Problems
Series-Parallel Calculations Part 1
Series Parallel Circuit Calculations
Problem No. 3 on Parallel Resonance in AC Circuit - AC Circuits - Basic Electrical Engineering
Parallel and Perpendicular Lines, Transversals, Alternate Interior Angles, Alternate Exterior Angles
Parallel Computing on Your Own Machine | Week 8 | 18.S191 MIT Fall 2020
Комментарии
 0:13:45
0:13:45
 0:05:45
0:05:45
 1:04:34
1:04:34
 0:14:06
0:14:06
 0:05:36
0:05:36
 0:18:21
0:18:21
 0:05:46
0:05:46
 0:04:24
0:04:24
 0:15:41
0:15:41
 0:10:01
0:10:01
 0:13:17
0:13:17
 0:06:47
0:06:47
 0:34:18
0:34:18
 0:12:29
0:12:29
 0:03:35
0:03:35
 0:33:43
0:33:43
 0:04:34
0:04:34
 0:05:55
0:05:55
 0:11:34
0:11:34
 0:15:27
0:15:27
 0:14:53
0:14:53
 0:07:36
0:07:36
 0:41:56
0:41:56
 0:21:12
0:21:12