filmov
tv
sqrt(i)
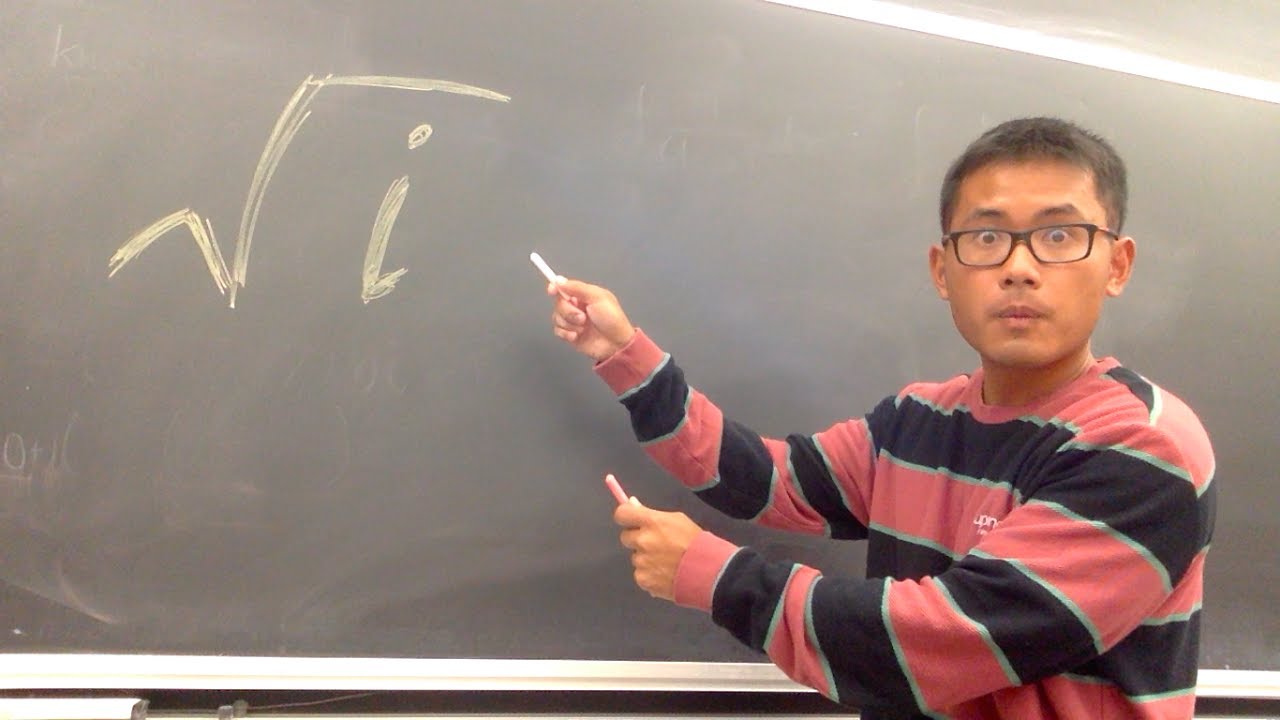
Показать описание
We will find both the square roots of i, i.e. sqrt(i). We will first write sqrt(i) as a complex number a+bi and then square both sides. Then we will solve for a and b by setting a system of equations! This is the algebra way to find the square root of the imaginary unit i.
Check out these related videos:
10% off with the code "WELCOME10"
Check out these related videos:
10% off with the code "WELCOME10"
sqrt(i)
This Is My New Favorite Number
sqrt(i^4)=?
A Wonderful Math Problem. Square root i + Square root -i =?
i-th root of i
sqrt(i+sqrt(i+sqrt(i+...))) = ?
Square root of i
sqrt(i)
Solving an International Olympiad Math Problem: Nested Square Root Challenge| First IMO-1959
sqrt(i) in polar form
why sqrt(36) is just positive 6
The square root of i || sqrt(i) || root i Explained
sqrt(i) | square root of i
sqrt(i) but ASMR
Finding sqrt(i)
5 simple unsolvable equations
A beautiful Olympiad Math Problem Sqrt. i | A Nice Olympiad Problem
sqrt(i) | How to find the square root of i
sqrt(i) as a complex number
sqrt(i) [Kurzversion]
A Proof That The Square Root of Two Is Irrational
Algebra 2 - Simplifying negative radicals using the the imaginary unit i, sqrt(-24)
sqrt(a+bi), how to get the square roots of a complex number
sqrt(i) - корень из мнимой единицы! // Математика
Комментарии
 0:09:02
0:09:02
 0:03:28
0:03:28
 0:01:10
0:01:10
 0:03:55
0:03:55
 0:01:52
0:01:52
 0:06:30
0:06:30
 0:03:10
0:03:10
 0:00:44
0:00:44
 0:02:34
0:02:34
 0:10:59
0:10:59
 0:01:42
0:01:42
 0:02:57
0:02:57
 0:01:28
0:01:28
 0:00:53
0:00:53
 0:03:28
0:03:28
 0:00:50
0:00:50
 0:10:55
0:10:55
 0:12:06
0:12:06
 0:04:42
0:04:42
![sqrt(i) [Kurzversion]](https://i.ytimg.com/vi/ntGPiCDklbM/hqdefault.jpg) 0:00:23
0:00:23
 0:17:22
0:17:22
 0:01:46
0:01:46
 0:07:54
0:07:54
 0:06:31
0:06:31