filmov
tv
A Wonderful Math Problem. Square root i + Square root -i =?
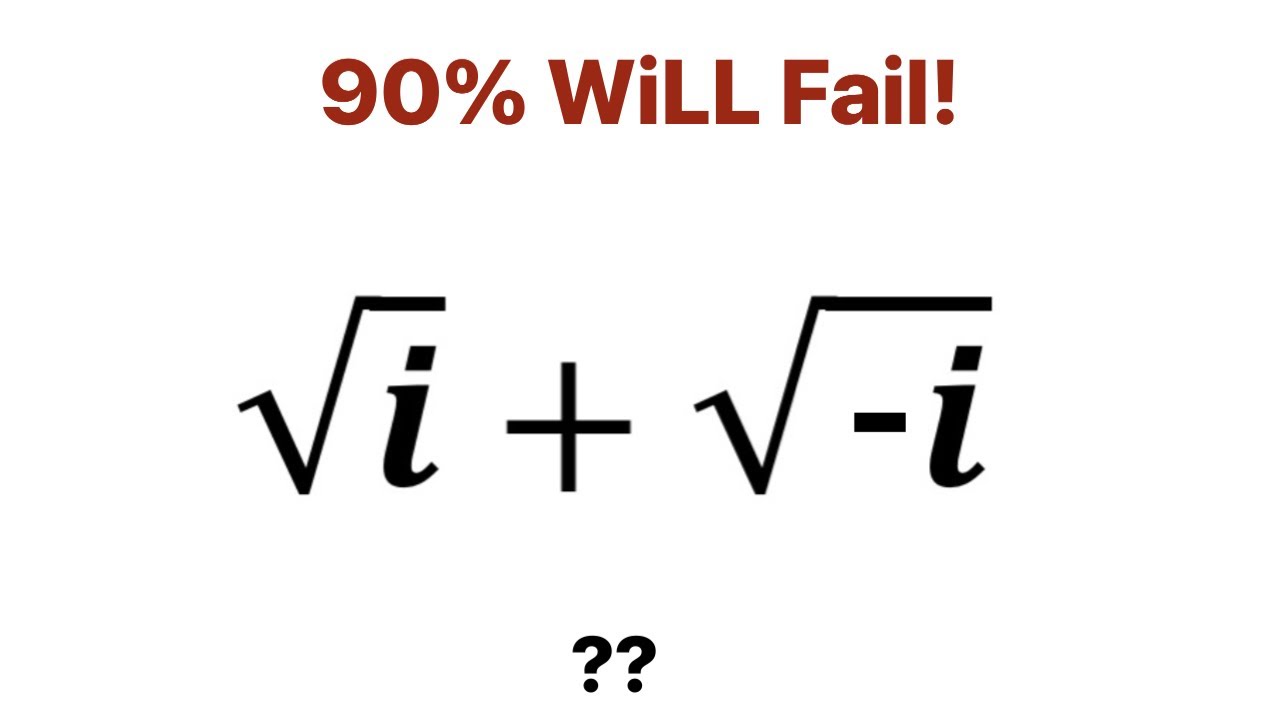
Показать описание
#maths #algebra #mathtricks #complex #complexnumbers
I am Rashel 👈👉I am a Math Tutor of youtube which can be called Online Math Tutor👍What is the answer of X in this exponential Equation?
A beautiful Math Problem ❤️A Nice Algebra Problem ❤️A Exponential Equation ❤️A Beautiful Math Problem ❤️Equation Solving ❤️Rashel's Classroom ❤️
❤️Equation ❤️Math Algebra.
I am Rashel 👈👉I am a Math Tutor of youtube which can be called Online Math Tutor👍What is the answer of X in this exponential Equation?
A beautiful Math Problem ❤️A Nice Algebra Problem ❤️A Exponential Equation ❤️A Beautiful Math Problem ❤️Equation Solving ❤️Rashel's Classroom ❤️
❤️Equation ❤️Math Algebra.
Maths problems With square #maths #shorts
The Simplest Math Problem No One Can Solve - Collatz Conjecture
Square Roots problems #maths #mathstricks #shorts
The Most Wholesome Math Equation
The Most Beautiful Equation in Math
Square Shortcut Trick🔥| Square 21-30 Tricks #math #shorts #shortvideo #short #trending #vedicmaths...
Luxembourg - Math Olympiad Question | You should know this trick
9 TIMES TABLE #shorts #math #maths #mathematics
Math Olympiad |Find the value of 'X+Y' in this equation #youtubeshorts #sorts #sortvideo
If you are a genius solve this! Math Game Challenge!!!
A Nice Square Root Problem | Find the value of a+b=? #olympiadmath #maths
Square Roots and Cube Roots | Math with Mr. J
Square Roots of Perfect Squares | Math with Mr. J
Learn to Square any 2 digit number I Math Tricks and Tips
How to Solve Quadratic Equations by Completing the Square? Grade 9 Math
Math trick for multiplying?
What are Square Roots? | Math with Mr. J
Mexico - A Nice Math Olympiad Exponential Problem
Math Antic - Simplifying Square Roots
HOW CHINESE STUDENTS SO FAST IN SOLVING MATH OVER AMERICAN STUDENTS
Speed Mental Math Exercise #shorts
Fast Multiplication Trick | Interesting math tricks #maths #shorts
How To Solve Math Percentage Word Problem?
United Kingdom - A Nice Exponential Equation | Math olympiad Question
Комментарии
 0:00:27
0:00:27
 0:22:09
0:22:09
 0:01:01
0:01:01
 0:00:16
0:00:16
 0:03:50
0:03:50
 0:00:19
0:00:19
 0:02:51
0:02:51
 0:00:23
0:00:23
 0:01:00
0:01:00
 0:00:28
0:00:28
 0:06:27
0:06:27
 0:05:03
0:05:03
 0:05:37
0:05:37
 0:07:10
0:07:10
 0:06:32
0:06:32
 0:00:16
0:00:16
 0:04:00
0:04:00
 0:08:36
0:08:36
 0:12:01
0:12:01
 0:00:23
0:00:23
 0:00:14
0:00:14
 0:00:28
0:00:28
 0:00:29
0:00:29
 0:09:19
0:09:19