filmov
tv
Square root of i

Показать описание
How to find the square root of i, as a complex number.
sqrt(i)
Square root of i
A Wonderful Math Problem. Square root i + Square root -i =?
Square root of i, explained Bob Ross style
What are Square Roots? | Math with Mr. J
Calculating Square Root by Hand (Early Grades)
Square roots explained Bob Ross style
Why is it called a SQUARE root?
Avoid this mistake when multiplying square roots with negative radicands‼️ #maths #algebra #shorts...
Introduction to square roots | Numbers and operations | 8th grade | Khan Academy
i-th root of i
Square Root Math Hack
How to Approximate Square Root of a Number
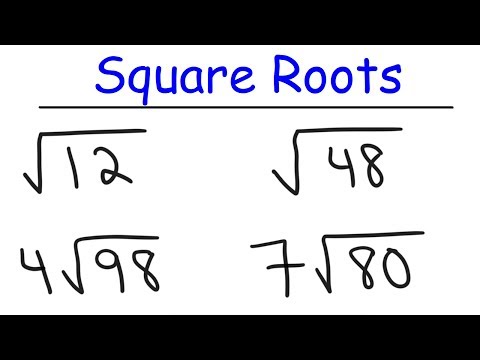
How To Simplify Square Roots
THE SQUARE ROOT 🚀 What is the Square Root? 👨🏻🚀 Math for Kids
This Is My New Favorite Number
A Proof That The Square Root of Two Is Irrational
How To Calculate Square Roots - Numerals That Changed Math Forever
Finding Square Roots of i | Complex Numbers
Find Square Root by Hand without Calculator
Math Antics - Exponents and Square Roots
What is the square root of – 1 ?
Addressing The Square-Root Confusion
Square root in 3 seconds - math trick
Комментарии
 0:09:02
0:09:02
 0:03:10
0:03:10
 0:03:55
0:03:55
 0:11:09
0:11:09
 0:04:00
0:04:00
 0:07:24
0:07:24
 0:10:55
0:10:55
 0:03:03
0:03:03
 0:00:57
0:00:57
 0:05:23
0:05:23
 0:01:52
0:01:52
 0:00:23
0:00:23
 0:00:52
0:00:52
 0:10:46
0:10:46
 0:05:13
0:05:13
 0:03:28
0:03:28
 0:17:22
0:17:22
 0:10:16
0:10:16
 0:09:19
0:09:19
 0:09:30
0:09:30
 0:11:09
0:11:09
 0:11:45
0:11:45
 0:14:32
0:14:32
 0:09:46
0:09:46