filmov
tv
Worked Probability Questions (2 of 3: Selecting sock pairs)

Показать описание
2 Examples of Probability With & Without Replacement
Finding probability example 2 | Probability and Statistics | Khan Academy
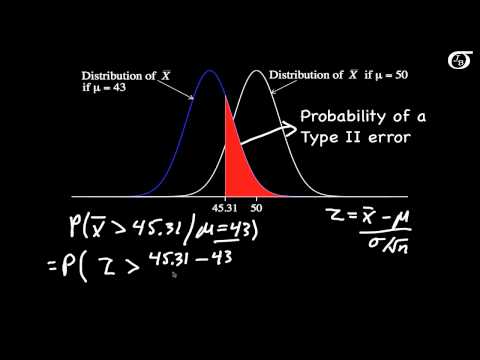
Calculating Power and the Probability of a Type II Error (A One-Tailed Example)
Math Antics - Basic Probability
KCSE 2019 - PROBABILITY
Finding probability example | Probability and Statistics | Khan Academy
WASSCE CORE MATHS NOV/DEC 2019 PROBABILITY
Test B (09 to 11) Solving Probability Word Problems Using Probability Formulas
1-Hour ADVANCED SAT Study
Multiplication & Addition Rule - Probability - Mutually Exclusive & Independent Events
L2.26.1. Functional Skills Maths Level 2: Work out the probability of combined events
How to Solve Probability Word Problems | P(A and B) | P(A or B) | Binomial Probability
Intro to Conditional Probability
Conditional Probability - Example 1
Probability you need for college!
All of Probability in 30 Minutes!! Foundation & Higher Grades 4-9 Maths Revision | GCSE Maths Tu...
Harder Probability Questions Forming and Solving Equations
Probability Tree Diagrams : removing items without replacement
Permutations, Combinations & Probability (14 Word Problems)
GCE 2020 paper 2 question 1(b) Probability
TSIA2 MATH SECTION: Probability Questions
Probability of Dice
Conditional Probability Example Problems
02 - Random Variables and Discrete Probability Distributions
Комментарии
 0:05:24
0:05:24
 0:09:56
0:09:56
 0:11:32
0:11:32
 0:11:28
0:11:28
 0:06:34
0:06:34
 0:02:56
0:02:56
 0:06:56
0:06:56
 0:20:36
0:20:36
 0:59:07
0:59:07
 0:10:02
0:10:02
 0:17:34
0:17:34
 0:16:21
0:16:21
 0:06:14
0:06:14
 0:08:12
0:08:12
 0:01:00
0:01:00
 0:38:22
0:38:22
 0:31:08
0:31:08
 0:03:19
0:03:19
 0:21:17
0:21:17
 0:05:25
0:05:25
 0:05:35
0:05:35
 0:02:44
0:02:44
 0:16:39
0:16:39
 0:29:54
0:29:54