filmov
tv
Solving an exponential system of equations

Показать описание
Solving Exponential Equations
Math Olympiad | How to Solve the System of Exponential Equations?
Solving an Exponential System in Two Ways
Exponential Equations - Algebra and Precalculus
Solving an exponential equation with different bases
Solving an exponential system of equations|Finding the value of (x- y)
System of Equations. One exponential, one linear..
Solving An Exponential System
Personalized EB-1A Guidance | Ankit Virmani, Namaswi Chandarana & Tina Gada | Conf42 PE 2024
Solving Simultaneous With Exponential directly.
Solve the Exponential System of Equations | Learn how to solve this Question without anxiety
Mathematical Olympiad | Solve system of Exponential Equations | Math Olympiad Training
Solving an Exponential System with Logarithms
solving exponential systems of equations / exponential equations
Olympiad Math | Learn how to solve the system of exponential equations | Math Olympiad Training
Solving an exponential system of equations
Solving an Exponential System in Two Ways
Solving Exponential Equation
Solving An Exponential System | Algebra
Solving Exponential Equation
how to solve an exponential equation with two different bases
How do you solve an exponential equation with e as the base
A Quick and Easy Exponential System
How to Solve Exponential Equations
Комментарии
 0:16:36
0:16:36
 0:03:59
0:03:59
 0:09:44
0:09:44
 0:05:58
0:05:58
 0:03:01
0:03:01
 0:04:52
0:04:52
 0:04:50
0:04:50
 0:00:37
0:00:37
 0:19:39
0:19:39
 0:13:50
0:13:50
 0:02:15
0:02:15
 0:08:30
0:08:30
 0:10:36
0:10:36
 0:07:29
0:07:29
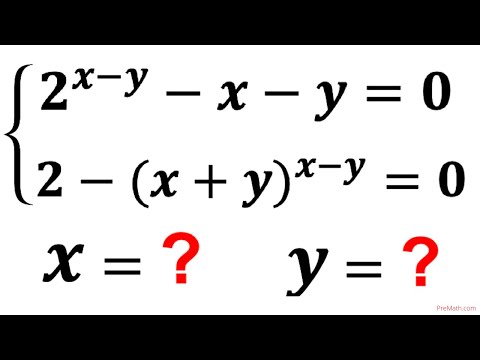 0:10:15
0:10:15
 0:08:09
0:08:09
 0:10:59
0:10:59
 0:02:56
0:02:56
 0:00:44
0:00:44
 0:00:56
0:00:56
 0:03:21
0:03:21
 0:02:47
0:02:47
 0:10:35
0:10:35
 0:05:05
0:05:05