filmov
tv
Math 391 Lecture 23 - Separation of Variables for PDEs and the Heat Equation
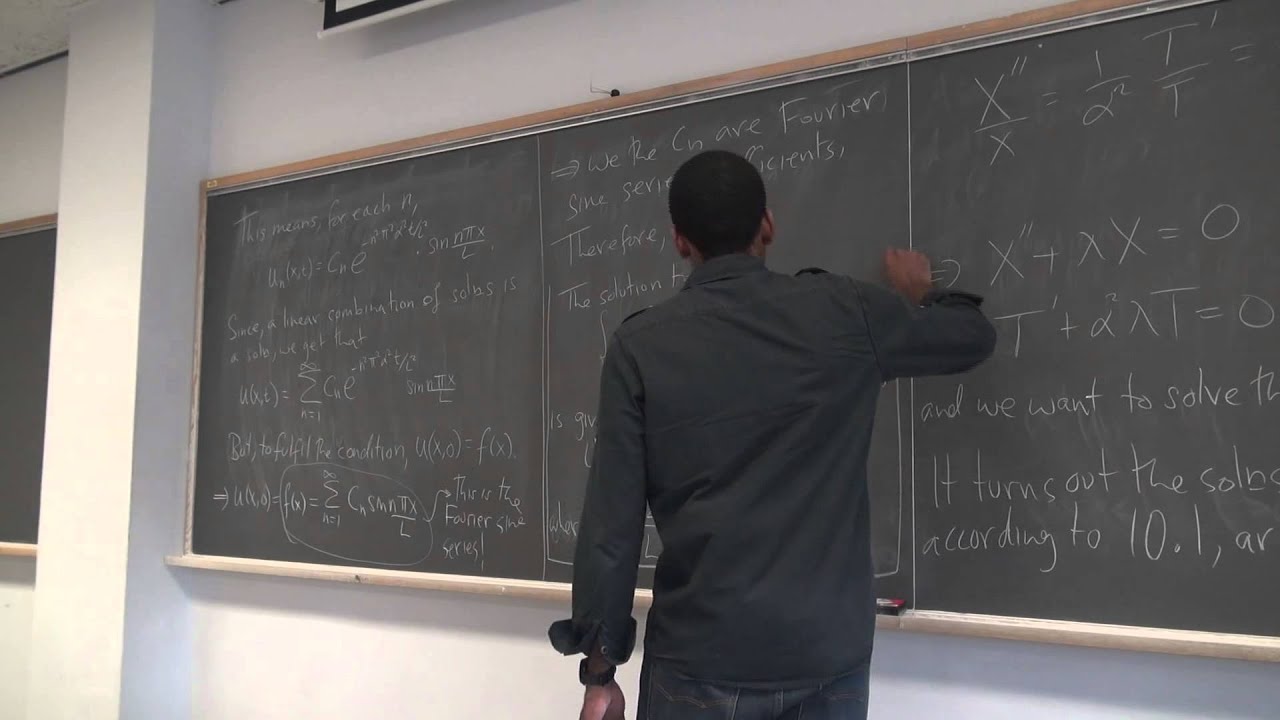
Показать описание
In this lecture we briefly look at an equation (a partial differential equation to be precise) that describes the conduction of heat through a rod. This is called the heat equation. We state the equation without proof, and then quickly look at an outline of how it is solved using separation of variables for the PDE.We obtain a general formula for the solution, and content ourselves with memorizing it and applying it from hence forth. As it turns out, the solution is a series solutions, having arbitrary constant coefficients given by the coefficients of a Fourier sine series.
This is the last official class of this semester. There may be a review session.
This is the last official class of this semester. There may be a review session.
Math 391 Lecture 23 - Separation of Variables for PDEs and the Heat Equation
Math 391 Lecture 22 - Fourier Series
Math 391 Lecture 7 - Chapter 2 HW review - part 1
Basics of Power Series Method | Differential Equations | Lecture 23
Math 391 Lecture 2 - Intro to differential equations - definitions and separation of variables
This is always divisible by 391??
Math 391 Lecture 19 - More series solutions, Euler Equations and Singular Points
Math 391 Lecture 18 - Series Solutions to second order linear differential equations contd
Math 391 1XC Lecture 7 - Misc ODEs;The Bernoulli First Order ODE, Complex Numbers; Euler's Iden...
Genius IQ Test-Maths Puzzles | Tricky Riddles | Maths Game | Paheliyan with Answers | Tricky Paheli
Math 391 Lecture 7 - Chapter 2 HW review - part 2
Math 346 Lecture 23 - Eigenvalues, eigenvectors, diagonalization and systems of linear ODEs
Indian vs Japanese Maths 🔥| Vedic Maths Trick for Fast Calculation | Speed Maths #trending #shorts...
Math 391 1XC Lecture 3 - Homogeneous First Order Differential Equations
Math 391 1XC Lecture 11 - More undetermined coefficients examples, and spring mass problems
Math 391 1XC Lecture 9 - Solutions to linear ODEs; Linear Independence and The Wronskian
Math 346 Lecture 4 - Systems of equations, row operations and the echelon forms
Math 1207-R03 Lecture 23 - Calculus with Parametric Curves; Arc Length; Intro to Polar Coordinates
Ek jhatke mein ho jayega The End 💔
Fast Percentage Trick
Math 391 Lecture 21 - Finding Laplace Transforms and using them to solve ODEs
Math 391 1XC Lecture 15 - Series Solutions of linear ODEs near Ordinary Points
CSCI550 - Lecture 1 (Part 1): Course Introduction
Lecture 23
Комментарии
 1:01:53
1:01:53
 1:07:16
1:07:16
 0:40:47
0:40:47
 1:36:41
1:36:41
 0:48:22
0:48:22
 0:07:14
0:07:14
 1:02:19
1:02:19
 1:04:18
1:04:18
 1:39:22
1:39:22
 0:00:24
0:00:24
 0:03:26
0:03:26
 1:04:39
1:04:39
 0:00:13
0:00:13
 1:16:41
1:16:41
 1:50:23
1:50:23
 1:45:34
1:45:34
 1:08:47
1:08:47
 1:15:42
1:15:42
 0:00:21
0:00:21
 0:00:52
0:00:52
 0:55:39
0:55:39
 1:04:48
1:04:48
 0:31:08
0:31:08
 1:12:57
1:12:57