filmov
tv
POURQUOI 1 = 0,999... ?

Показать описание
-•--•---• Médématiques sur Internet •---•--•-
💰 Médéboutique :
🎁 PayPal :
✉️ E-mail :
🔔Discord :
🎥 Chaîne secondaire :
📘 Facebook :
😺 Scratch :
📚 Médéliste Révisions :
Idéal pour réviser avant un examen !
🥰 Médéliste Thèmes :
Idéal pour retrouver tes sujets de maths préférés !
🎵 TikTok :
👨🏫 Superprof :
-•--•---• ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ •---•--•-
Besoin de me contacter pour une demande commerciale, une question de maths, un conseil, un avis, ou pour toute autre raison ?
N'hésite pas à me contacter par mail, via Messenger, ou encore via Discord (voir ci-dessus). 😋
@sushinihiliste Si tu veux, il y a de belles pépites dans les commentaires ! 😘
💰 Médéboutique :
🎁 PayPal :
✉️ E-mail :
🔔Discord :
🎥 Chaîne secondaire :
📘 Facebook :
😺 Scratch :
📚 Médéliste Révisions :
Idéal pour réviser avant un examen !
🥰 Médéliste Thèmes :
Idéal pour retrouver tes sujets de maths préférés !
🎵 TikTok :
👨🏫 Superprof :
-•--•---• ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ •---•--•-
Besoin de me contacter pour une demande commerciale, une question de maths, un conseil, un avis, ou pour toute autre raison ?
N'hésite pas à me contacter par mail, via Messenger, ou encore via Discord (voir ci-dessus). 😋
@sushinihiliste Si tu veux, il y a de belles pépites dans les commentaires ! 😘
Pourquoi 1=0,999999999... ?
0,999…=1,000…. !! T’en penses quoi ??? #prof #professeur #maths #mathematiques #ecole #college #lyc...
POURQUOI 1 = 0,999... ?
Pourquoi 0, 999... est égal à 1 ?
Pourquoi 0,9999….=1. / Démonstration
0,99999.... = 1. Vrai ou faux ?
Every PROOF you've seen that .999... = 1 is WRONG
0.9 Repeating Equal to 1 Algebraic Proof | Fun Math JusticeTheTutor #shorts #maths #math
0,9999... = 1 ??? Infini 2
les nombres de 10 000 a 999 999
BACKROOM LVL 188 !! (Real footage)
Les nombres entiers
XP illimité 🤯
French numbers 1-100 (Learn French With Alexa)
J’ai eu des robux gratuit#freerobux
How Juice Wrld died 😢
TOUTES LES RÉCOMPENSES de la saison 22 !!
Le niveau des joueurs fortnite selon les années ! #shorts
Scp 173 CRUNCH
la vrai tête de zetfar
what 1000hrs of aim training looks like
Why Prices Ending in .99 Are Fooling Your Brain
Super Mario, Bowser & Princess Peach LOVES Coco Pops. #supermario #mariobros #princesspeach
How Does Your Body Turn Food Into Poop? 💩
Комментарии
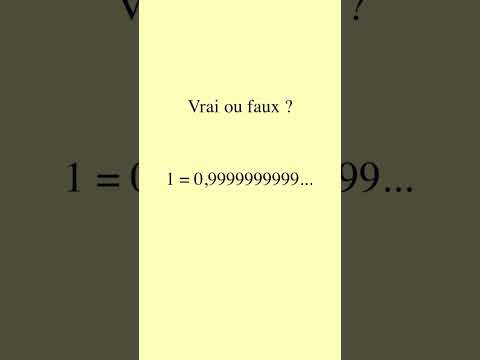 0:01:00
0:01:00
 0:01:43
0:01:43
 0:00:57
0:00:57
 0:02:38
0:02:38
 0:03:32
0:03:32
 0:02:46
0:02:46
 0:09:25
0:09:25
 0:01:01
0:01:01
 0:15:45
0:15:45
 0:03:26
0:03:26
 0:00:16
0:00:16
 0:02:38
0:02:38
 0:00:23
0:00:23
 0:04:08
0:04:08
 0:00:28
0:00:28
 0:00:30
0:00:30
 0:00:36
0:00:36
 0:00:23
0:00:23
 0:00:06
0:00:06
 0:00:09
0:00:09
 0:00:10
0:00:10
 0:02:33
0:02:33
 0:00:11
0:00:11
 0:00:39
0:00:39