filmov
tv
Solving A Nice Factorial Equation

Показать описание
🤩 Hello everyone, I'm very excited to bring you a new channel (aplusbi)
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
When you purchase something from here, I will make a small percentage of commission that helps me continue making videos for you.
If you are preparing for Math Competitions and Math Olympiads, then this is the page for you!
CHECK IT OUT!!! ❤️ ❤️ ❤️
INFINITE SERIES:
If you need to post a picture of your solution or idea:
#radicals #radicalequations #algebra #calculus #differentialequations #polynomials #prealgebra #polynomialequations #numbertheory #diophantineequations #comparingnumbers #trigonometry #trigonometricequations #complexnumbers #math #mathcompetition #olympiad #matholympiad #mathematics #sybermath #aplusbi #shortsofsyber #iit #iitjee #iitjeepreparation #iitjeemaths #exponentialequations #exponents #exponential #exponent #systemsofequations #systems
#functionalequations #functions #function #maths #counting #sequencesandseries
#algebra #numbertheory #geometry #calculus #counting #mathcontests #mathcompetitions
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
When you purchase something from here, I will make a small percentage of commission that helps me continue making videos for you.
If you are preparing for Math Competitions and Math Olympiads, then this is the page for you!
CHECK IT OUT!!! ❤️ ❤️ ❤️
INFINITE SERIES:
If you need to post a picture of your solution or idea:
#radicals #radicalequations #algebra #calculus #differentialequations #polynomials #prealgebra #polynomialequations #numbertheory #diophantineequations #comparingnumbers #trigonometry #trigonometricequations #complexnumbers #math #mathcompetition #olympiad #matholympiad #mathematics #sybermath #aplusbi #shortsofsyber #iit #iitjee #iitjeepreparation #iitjeemaths #exponentialequations #exponents #exponential #exponent #systemsofequations #systems
#functionalequations #functions #function #maths #counting #sequencesandseries
#algebra #numbertheory #geometry #calculus #counting #mathcontests #mathcompetitions
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Solving A Nice Factorial Equation
Nice Factorial Equation - Can You Solve It?
A nice factorial equation: The math behind solving equations.
Can We Solve A Nice Factorial Equation
A Nice Factorial Equation
Let's Solve A Nice Factorial Equation
Germany | A nice Factorial Equation | Math Olympiad Algebra Problem | Can you solve this ? Simplify.
A Nice Math Factorial Problem • Evaluate #shorts #olympiad #mathematics #maths #matholympiad #tips
What Is Recursion In Python? | Python Recursion Tutorial #python
Math Olympiad Preparation | A Nice Factorial Problem | Calculate Without Calculators...
a nice factorial equation.
a nice factorial problem
A Nice Factorial Equation | n!=2^n
Sweden | A nice factorial equation | Math Olympiad | Can You Solve
how to solve a factorial equation?
USA | A nice factorial equation | math Olympiad problem
Can You Solve this Factorial Equation? | Fast & Easy Tutorial
A Beautiful Exponential Problem Olympiad Math || A Nice Factorial Equation
Math Olympiad | A Nice Algebra Problem | A Nice Factorial Equation
what is the value of X ? | A nice factorial equation to solve
China | Math Olympiad Factorial | A Nice Algebra Problem 👇👇👇
A mysterious factorial equation.
A Wonderful Factorial Maths Problem. Solve For X?
Solving A Nice Factorial Math Equation || Find the Value of n || Olympiad Math | n!@TheMathScholar23
Комментарии
 0:03:19
0:03:19
 0:04:43
0:04:43
 0:10:54
0:10:54
 0:09:31
0:09:31
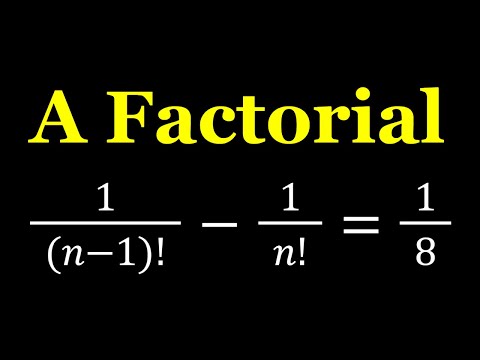 0:08:38
0:08:38
 0:10:28
0:10:28
 0:12:42
0:12:42
 0:00:40
0:00:40
 0:07:43
0:07:43
 0:06:19
0:06:19
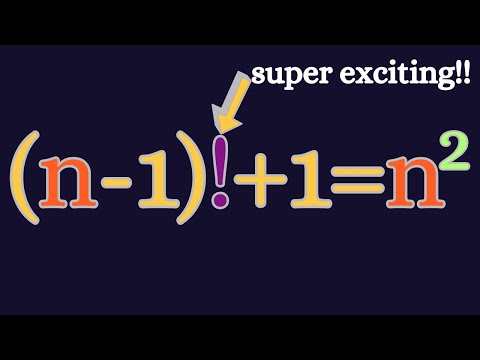 0:10:16
0:10:16
 0:00:37
0:00:37
 0:09:32
0:09:32
 0:07:23
0:07:23
 0:02:22
0:02:22
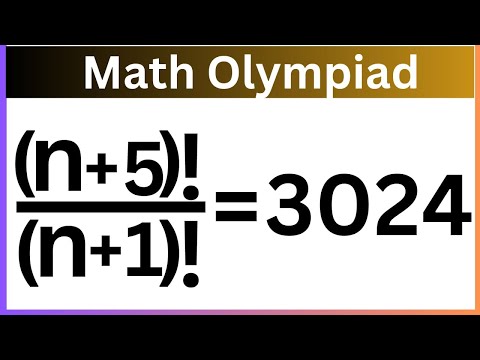 0:11:10
0:11:10
 0:04:45
0:04:45
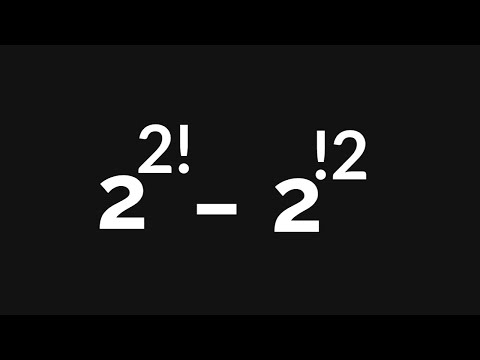 0:02:57
0:02:57
 0:08:07
0:08:07
 0:03:37
0:03:37
 0:09:42
0:09:42
 0:14:28
0:14:28
 0:02:13
0:02:13
 0:06:04
0:06:04