filmov
tv
Self Study Galois Theory
Показать описание
Do you want to study Galois theory, but you can't take a regular class? Here is self study guide based on the resources I found most helpful when I independently studied Galois theory. If you haven't already, check out my video called "Self Study Strategies for Math" so you know how to turn the resources from this video into a successful self study.
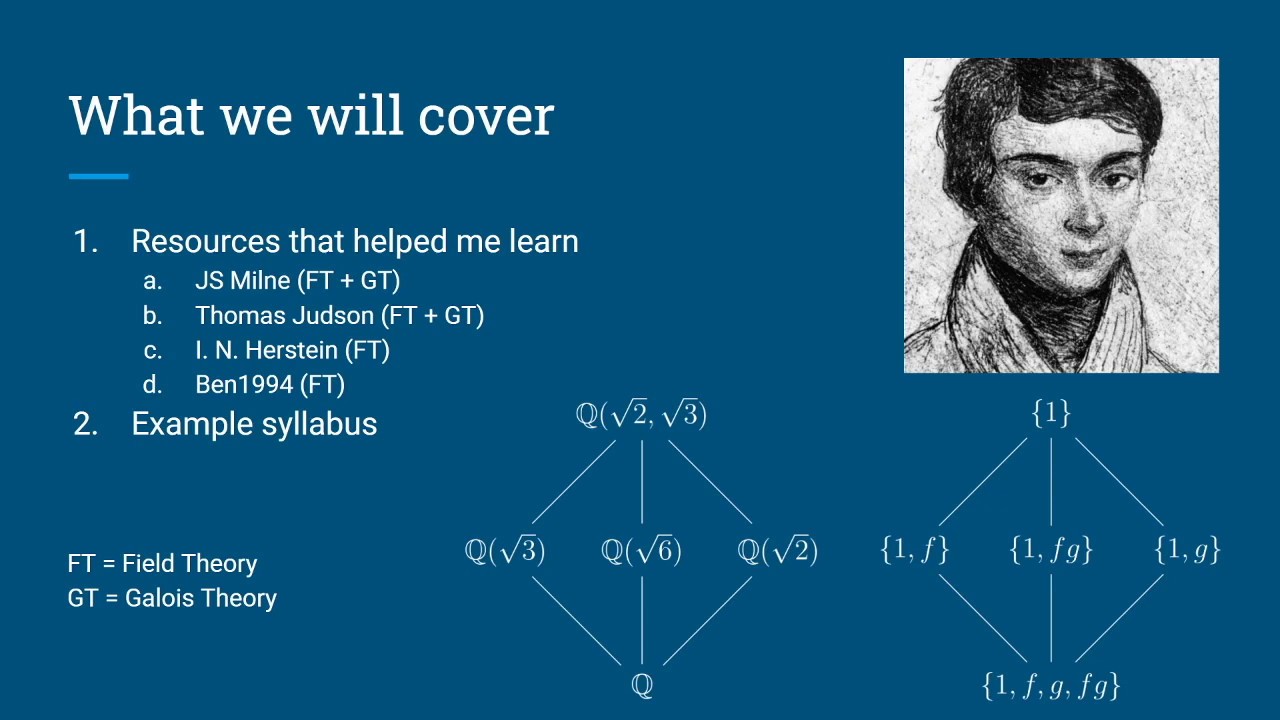
Links:
Example Syllabus:
Do Milne exercises last, they will be the hardest.
Textbooks:
Abstract Algebra: Theory and Applications
Abstract Algebra by I. N. Herstein
Weeks:
1. Read 1 - 20 from Milne (stops before Constructions) and do exercises 1, 8 from Herstein 5.3 (p. 230 and 231) and 5 and 7 from Herstein 5.4 (p. 234) and 1-1, 1-2, and 1-3 from Milne (p. 25)
2. Read 20 - 30 and do exercises 1-4 and 1-6 from Milne (p. 25) and 6, 7, 8, 9, and 14 from Herstein 5.6 (p. 249)
Topics covered:
fields, polynomial rings, extension fields, algebraic and transcendental numbers, constructions with straight-edge and compass, splitting fields, Galois groups, fundamental theorem of Galois Theory, computing Galois groups, insolubility of the quintic
Description:
This is a follow-on course to 18.703 to add elements of Galois Theory into the structure of 18.703. It takes a more traditional approach to Galois Theory than 18.702.
Links:
Example Syllabus:
Do Milne exercises last, they will be the hardest.
Textbooks:
Abstract Algebra: Theory and Applications
Abstract Algebra by I. N. Herstein
Weeks:
1. Read 1 - 20 from Milne (stops before Constructions) and do exercises 1, 8 from Herstein 5.3 (p. 230 and 231) and 5 and 7 from Herstein 5.4 (p. 234) and 1-1, 1-2, and 1-3 from Milne (p. 25)
2. Read 20 - 30 and do exercises 1-4 and 1-6 from Milne (p. 25) and 6, 7, 8, 9, and 14 from Herstein 5.6 (p. 249)
Topics covered:
fields, polynomial rings, extension fields, algebraic and transcendental numbers, constructions with straight-edge and compass, splitting fields, Galois groups, fundamental theorem of Galois Theory, computing Galois groups, insolubility of the quintic
Description:
This is a follow-on course to 18.703 to add elements of Galois Theory into the structure of 18.703. It takes a more traditional approach to Galois Theory than 18.702.
0:05:54
Self Study Galois Theory
0:09:53
How to self study pure math - a step-by-step guide
0:00:23
Galois Theory by Emil Artin #shorts
0:04:16
19 Galois: Galois Theory, Non-solvable Quintic by Home of Mathematics
0:03:54
Most Psychedelic Math Book 'Galois Theory by Emil Artin'
0:10:19
The Insolvability of the Quintic
0:14:41
Teaching myself abstract algebra
0:00:31
Galois Theory?
0:00:38
Why greatest Mathematicians are not trying to prove Riemann Hypothesis? || #short #terencetao #maths
0:45:24
Why you can't solve quintic equations (Galois theory approach) #SoME2
0:03:22
Grant Sanderson (3Blue1Brown): Best Way to Learn Math | AI Podcast Clips
0:04:08
Self Study Map of Mathematics
0:25:10
What is the square root of two? | The Fundamental Theorem of Galois Theory
0:49:37
Online Courses #17 - Model Theory (Infinite Galois Theory I) by Piotr Kowalski
0:52:04
A short Introduction to Galois Theory
0:16:11
What are...the groups of Galois theory?
0:15:08
Learn Abstract Algebra from START to FINISH
0:24:34
Galois theory: Introduction
0:33:43
Galois Theory For Beginners/Dummies (Like myself)
0:05:21
Self Study Abstract Algebra
0:40:36
Lean Together 2021: Galois Theory
0:47:25
Field and Galois Theory: 01 Introduction, Field Extensions
0:03:20
Application of Galois Theory
0:28:44
Unlocking the Mysteries of Galois Extensions | Galois Theory | Mastering Advanced Field Theory
Комментарии