filmov
tv
What is the square root of two? | The Fundamental Theorem of Galois Theory
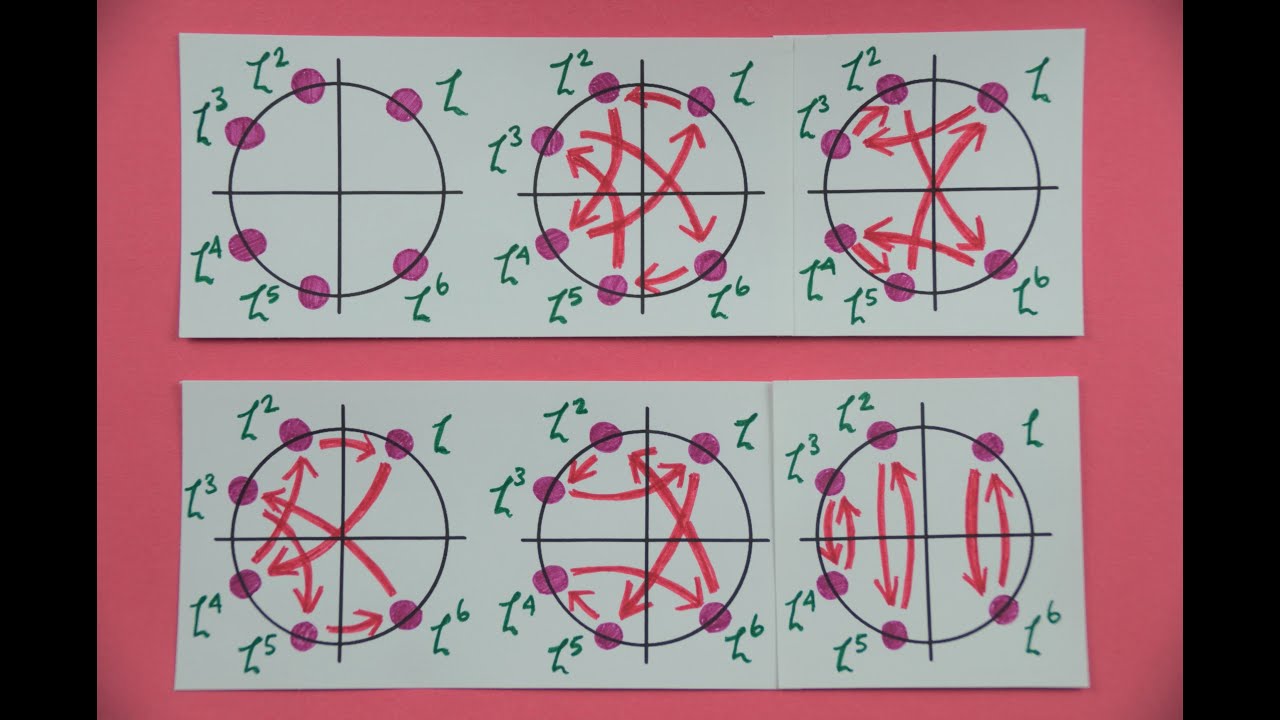
Показать описание
This video is an introduction to Galois Theory, which spells out a beautiful correspondence between fields and their symmetry groups.
__
SOURCES and REFERENCES for Further Reading!
This video is a quick-and-dirty introduction to Galois theory. But as with any quick introduction, there are details that I gloss over for the sake of brevity. To learn these details rigorously, I've listed a few resources down below.
(a) Galois Theory
(b) Group Theory
MUSIC CREDITS:
The song is called “Taking Flight”, by Vince Rubinetti.
THANK YOUs:
Extra special thanks to Davide Radaelli and Grant Sanderson for helpful conversations while making this video!
SOFTWARE USED:
Adobe Premiere Pro for Editing
Follow me!
Twitter: @00aleph00
Instagram: @00aleph00
Intro: (0:00)
What is the square root of 2?: (1:08)
Fields and Automorphisms: (6:04)
Examples: (8:55)
Group Theory: (16:34)
The Fundamental Theorem: (18:25)
__
SOURCES and REFERENCES for Further Reading!
This video is a quick-and-dirty introduction to Galois theory. But as with any quick introduction, there are details that I gloss over for the sake of brevity. To learn these details rigorously, I've listed a few resources down below.
(a) Galois Theory
(b) Group Theory
MUSIC CREDITS:
The song is called “Taking Flight”, by Vince Rubinetti.
THANK YOUs:
Extra special thanks to Davide Radaelli and Grant Sanderson for helpful conversations while making this video!
SOFTWARE USED:
Adobe Premiere Pro for Editing
Follow me!
Twitter: @00aleph00
Instagram: @00aleph00
Intro: (0:00)
What is the square root of 2?: (1:08)
Fields and Automorphisms: (6:04)
Examples: (8:55)
Group Theory: (16:34)
The Fundamental Theorem: (18:25)
What are Square Roots? | Math with Mr. J
THE SQUARE ROOT 🚀 What is the Square Root? 👨🏻🚀 Math for Kids
Why is it called a SQUARE root?
Square roots explained Bob Ross style
Math Antics - Exponents and Square Roots
Introduction to square roots | Numbers and operations | 8th grade | Khan Academy
What is a Square Root and a Perfect Square?
Introduction to Square Roots
Square Root Math Hack
Square Roots and Cube Roots | Math with Mr. J
Do you remember the square roots of these perfect squares? 🤯 #Shorts #math #maths #mathematics
A Proof That The Square Root of Two Is Irrational
What are Square Roots? | Exponents | Best Square Root Tricks | Don't Memorise
How To Find The Square Root of Large Numbers Mentally
How To Simplify Square Roots
How To Calculate Square Roots - Numerals That Changed Math Forever
What is the square root of – 1 ?
How to Approximate Square Root of a Number
Square root of i
Math Antic - Simplifying Square Roots
Simplifying Square Roots | Math with Mr. J
Calculating Square Root by Hand (Early Grades)
Cube Root Math Trick
Square Roots of Perfect Squares | Math with Mr. J
Комментарии
 0:04:00
0:04:00
 0:05:13
0:05:13
 0:03:03
0:03:03
 0:10:55
0:10:55
 0:11:09
0:11:09
 0:05:23
0:05:23
 0:06:38
0:06:38
 0:04:14
0:04:14
 0:00:23
0:00:23
 0:05:03
0:05:03
 0:00:11
0:00:11
 0:17:22
0:17:22
 0:04:11
0:04:11
 0:12:37
0:12:37
 0:10:46
0:10:46
 0:10:16
0:10:16
 0:11:45
0:11:45
 0:00:52
0:00:52
 0:03:10
0:03:10
 0:12:01
0:12:01
 0:07:44
0:07:44
 0:07:24
0:07:24
 0:00:12
0:00:12
 0:05:37
0:05:37