filmov
tv
Factor ANY Quadratic Equation Without Guessing | Outlier.org

Показать описание
What if you could solve any quadratic function without any guess-and-check or memorization? This method was actually known by the Babylonians nearly 2,000-3,000 years ago but it's hardly taught in schools. Po-Shen Loh shares how to use the technique, the moment he discovered it, and why it's still such a secret.
About @OutlierOrg :
#Precalculus #Po-ShenLoh #FactoringMethod #Outlier
About @OutlierOrg :
#Precalculus #Po-ShenLoh #FactoringMethod #Outlier
Factor ANY Quadratic Equation Without Guessing | Outlier.org
Factoring Quadratics in 5 seconds! Trick for factorising easily
A Brilliant way to factorise ANY Quadratic Equation without finding factors 😱😱😱🤩🤩🤩
How to Factor any Quadratic Equation Easily - Trick for factorising
How To Solve Quadratic Equations By Factoring - Quick & Simple! | Algebra Online Course
Quadratic Equations | Solve by factoring | Free Math Videos
Solve Quadratic Equations By Factoring - Simple Trick No Fuss!
Find Factors of Any Quadratic Equation|Short Trick|CBSE Maths|Competitive Exams|@simplemathslogics
Quadratic equations:x2+12x+35=0 Algebra factor questions #mathshorts #MohmmadShaheedsajoAli🕋Allah...
Solving Without Factoring or Quadratic Formula
How to Factor and Solve Quadratics - Sneaky Trick - No Fuss Factoring
The Better Quadratic Formula You Won't Be Taught
How To Factor Any Quadratic Equation Using The Quadratic Formula
FASTEST way to factor a trinomial! #shorts
Factoring Quadratics... How? (NancyPi)
Quadratic Equation Shortcut Trick | Solve Equation in 5 Seconds
How to Factor and Solve Quadratic Trinomials - No Fuss Factoring - Quick Math Trick
Solve quadratic equation by factorisation
Learn the ac method for factoring and solving a quadratic equation
How to identify when a trinomial is not factorable
Factoring Quadratic Expressions Pt. 1
How To Factor Difficult Quadratic Equations
Factor Any Quadratic Slow
Solving Quadratic Equations by Factoring│Algebra
Комментарии
 0:14:02
0:14:02
 0:10:57
0:10:57
 0:08:11
0:08:11
 0:06:44
0:06:44
 0:12:29
0:12:29
 0:02:43
0:02:43
 0:06:31
0:06:31
 0:08:00
0:08:00
 0:00:41
0:00:41
 0:00:58
0:00:58
 0:05:42
0:05:42
 0:03:02
0:03:02
 0:05:16
0:05:16
 0:00:55
0:00:55
 0:09:14
0:09:14
 0:00:30
0:00:30
 0:03:54
0:03:54
 0:09:05
0:09:05
 0:05:00
0:05:00
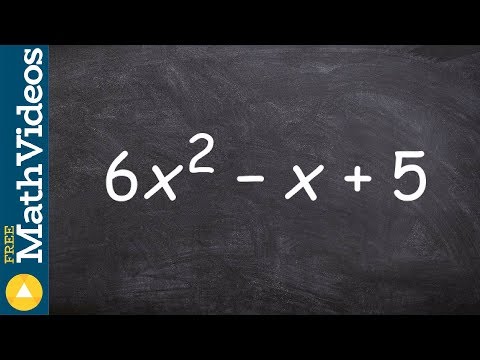 0:01:38
0:01:38
 0:05:53
0:05:53
 0:05:47
0:05:47
 0:10:24
0:10:24
 0:22:30
0:22:30