filmov
tv
Find the overlapping area -- not easy!

Показать описание
If you are going to use an ad-blocker, considering using brave and tipping me BAT!
Books I like:
Abstract Algebra:
Differential Forms:
Number Theory:
Analysis:
Calculus:
My Filming Equipment:
Find the overlapping area -- not easy!
C1 Overlapping Figures
Area of Overlapping Figures (6th Grade)
Find the Area of Overlapping Rectangles in Python
8.1g Find area with overlapping
Calculate overlapping land area in QGIS
31) Find overlapping area. #maths #matholympiad #geometry
Tricky Question on Overlapping Area Solved!
QGIS Calculate Overlapping Areas & Topology
Geometry, Level 3 of 6, Example 2, Overlapping circles
What is the overlapping area when you rotate a right triangle?
Area of Overlapping Shapes
Two overlapping squares of different length, find the area of shaded region
Area between Overlapping Circles inside Square
AREA OF OVERLAPPING CIRCLES
Can You Solve This Shaded Area? | Mystery of 2 Overlapping Squares
Finding the Area Between Two Curves by Integration
Perimeter of overlapping circles (A-level)
Video 5 Primary 6 Circles with Overlapping Area
Overlapping area of ellipses.
P6 Area and Perimeter - Best Way To Solve An Overlapping Shape | DO IT WITH ME
Two overlapping squares
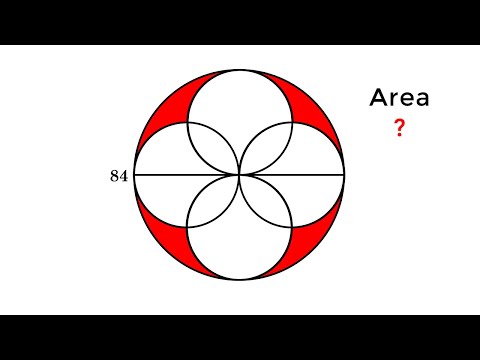
4 Overlapping Circles Puzzle
Overlapping Rectangles | 6Company 30 Days Challenge | Goldman Sachs 🔥 | #ReviseWithArsh
Комментарии
 0:10:21
0:10:21
 0:01:48
0:01:48
 0:09:30
0:09:30
 0:11:36
0:11:36
 0:03:14
0:03:14
 0:03:16
0:03:16
 0:01:00
0:01:00
 0:02:59
0:02:59
 0:12:41
0:12:41
 0:05:58
0:05:58
 0:04:34
0:04:34
 0:06:16
0:06:16
 0:04:14
0:04:14
 0:01:48
0:01:48
 0:07:54
0:07:54
 0:09:19
0:09:19
 0:07:52
0:07:52
 0:11:06
0:11:06
 0:06:05
0:06:05
 0:08:45
0:08:45
 0:04:33
0:04:33
 0:07:13
0:07:13
 0:07:29
0:07:29
 0:02:16
0:02:16