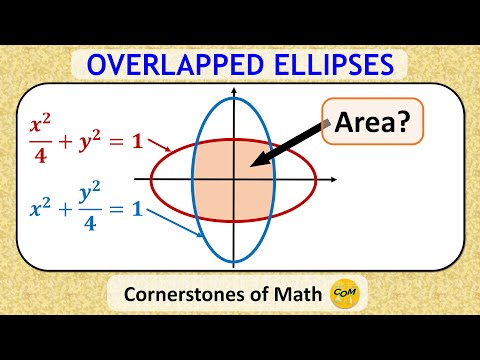
Overlapping area of ellipses.

If you are going to use an ad-blocker, considering using brave and tipping me BAT!

Books I like:

Abstract Algebra:

Differential Forms:

Number Theory:

Analysis:

Calculus:

My Filming Equipment:

[zactron]

I like this a lot, it explains why the area of an elipse is just Pi × ab, because it's effectively Pi r^2 but in a warped space where r is length a in one direction, and length b in the other.

[anonymous_]

Shrink the x axis by a and y axis by b. Now the original area becomes the area of the sector of a unit circle with angle Area of this sector=(1/2)arctan(a/b). So area of the original portion =(ab/2)×arctan(a/b).

[kriswillems]

You don't need calculus for this. The area is just the area of a circle segment that is scaled up in one direction, so the area is the area of a circle segment multiplied with that scale factor (b/a).

[kevinmartin]

Starting at 4:10 I was a bit lost until I figured out that the r and theta have nothing to do with the diagram drawn at the top right. Until then I was wondering why theta didn't just go from 0 to pi/4.

This method seemed complicated, after all, the answer is just 4 times the area under the green ellipse from -c to c minus 4c^2 (the area of the square that this counted twice). But then when you get into solving for c and writing out and solving the integral, things end up just as complicated as the method presented here.

[general_paul]

I had this assignment in my final year of high school where I was supposed to derive the relation and frame an application based question and solve it

[txikitofandango]

Okay, before watching this, I have this idea.
Draw the line y = x. The area of the shaded region bounded by y=x, the two ellipses, and the x axis is 1/8 the shaded region.
The curves intersect at x = ab/√(a²+b²).
So you just need the integral from ab/√(a²+b²) to a of b√(1-x²/a²) dx + the area of the triangle with base and height ab/√(a²+b²). Then whole thing times 8.

[engjayah]

Without Double Integral:
Area of Region R = Integration from 0 to pi/4 of {(1/2)r^2}d(theta) where r stands for the polar form of RED ellipse.
Which is r = ab/[Sqr(b^2cos^(thea) + a^2sin(theta)]
This will avoid the complicated double integration and final answer A = 8R = 4ab*arctan (b/a)

[manucitomx]

I very much enjoyed this problem. I have a thing for ellipses, perhaps because of my body shape.
Thank you, professor.

[artsmith]

If we can solve for c, then the total area is 4 * integral (from x=0 to x=c for the region between y=0 and the green ellipse) plus 4 * integral (from x=c to x=a for the region between y=0 and the pink ellipse)

[spacesurfer]

I figured this out using the polar form of the ellipse and a little help from Wolfram with intergration.
First, realize that in the polar form, area from angle 0 to pi/4 is 1/8 of the total area we are looking for because of symmetry.
The polar form of ellipse is r = sqrt(ab/((b*cos(t))^2+(a*sin(t))^2), where t is the angle. The area is 1/2 integrate r^2.
So area is 1/2 integrate and take from 0 to pi/4.
And you get (using Wolfram) ab(artcan(a*tan(t)/b))/2 which equal ab(arctan(a/b))/2 when applying pi/4.
Now multiply by 8 and you get above.

[leeya]

resolve congruent system x congruent1(mod6), x congruent5(mod14), x congruent4(mod21)

[polarisator]

My solution: Integrate y=f(x) = a*sqrt(1-(x/b)^2) from 0 to a*b/sqrt(a^2+b^2), to get the area underneath the "broad" elipse from x = 0 to the interception. You need some substitution x =b * sin(u) --> dx = b * cos(u)*du --> a*sqrt(1-(x/b)^2)*dx = = a*b* (cos(u))^2*du =a*b/2*(1+cos(2u))*du =
= a*b/2 * d(u+1/2*sin(2*u)) = a*b/2*d(u+sin(u)*cos(u))
integrating over u goes from 0 to arcsin(a/sqrt(a^2+b^2)) ; (0<u<pi/2)
You get an Area +ab/(a^2+b^2) = a*b/2*arctan(a/b) + a^2*b^2/(a^2+b^2)/2
The overlapping area in one quadrant is (due to symmetry) A/4=2*A1-A2 = a*b*arctan(a/b); where A2= a^2*b^2/(a^2+b^2) is the area of the square.

--> A = 4*a*b*arctan(a/b)

[thedarkknight]

So finally you made a video on Conics 😎🙏

[lucaromanelli]

R should be equal to the area of triangle 0, 0;c, c;c, 0 (0, 5c^2) + integral x[c, a] (b/a)*sqr(a^2-x^2)dx

[guilhermefranco]

Next on Michael Penn series: perimeter of an ellipse blindfolded

[anshumanagrawal]

Is there a way to do this without the double Integration stuf

[elidamon]

It seems like you should be able to do this without the integration using Euclidean geometry. The area of the elliptical sector is a/b times the area of a circular sector.

[atrumluminarium]

Isn't arctan(a/b) always 45° in this case?

[arthurbrietzke]

Please help me. How to solve: integral (x^2)/(sqrt((x^2)+64))
I didn't find clear videos and even the calculator is giving different results for this calculation.

[davidmeijer]

Very closely related to, well it reminds me of, PRoject Euler, CrissCrossEllipses problem….help!!! Can’t get the 106th case of the Canonical Elliptical Triples for the second test case in the problem….got the other 105!!! Argh!