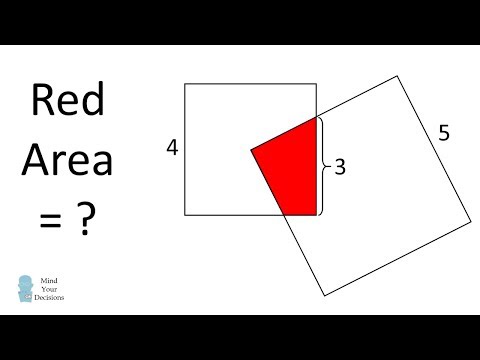
Two overlapping squares of different length, find the area of shaded region

preview_player
Показать описание
Two overlapping squares of different length, find the area of shaded region
  1. SSCSelector
  2. Geometry
  3. Mathematics
  4. International Mathematics Olympiad
  5. Math Olympiad
  6. Maths Questions
Рекомендации по теме
Two overlapping squares 0:04:14

Two overlapping squares of different length, find the area of shaded region

Two overlapping squares 0:07:13

Two overlapping squares

The two overlapping 0:15:47

The two overlapping rectangles shown have the same width, but different lengths.

Can YOU Solve 0:01:20

Can YOU Solve Overlapping Squares Problem?

C1 Overlapping Figures 0:01:48

C1 Overlapping Figures

How To Solve 0:03:47

How To Solve The Overlapping Squares Riddle

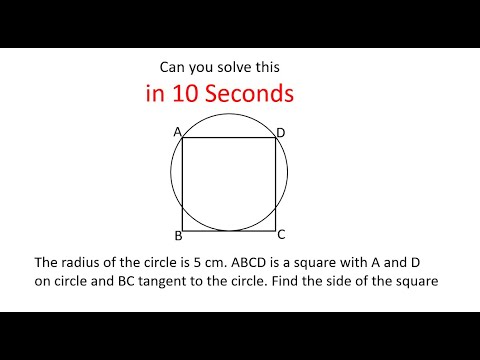
A square and 0:04:00

A square and a circle are overlapping each other

Area of Overlapping 0:09:30

Area of Overlapping Figures (6th Grade)

Spiderweb Math - 0:01:35

Spiderweb Math - Area and Perimeter 2 (Overlapping Squares 2)

Can You Solve 0:02:16

Can You Solve The Overlapping Squares Riddle?

Area between Overlapping 0:01:48

Area between Overlapping Circles inside Square

🔑 Shaded Area 0:26:15

🔑 Shaded Area in Overlapping Squares HARD problem ! ! ! ! !

P6 Area and 0:04:33

P6 Area and Perimeter - Best Way To Solve An Overlapping Shape | DO IT WITH ME

Overlapping squares 2022 0:03:24

Overlapping squares 2022 02 19

Area of Overlapping 0:06:16

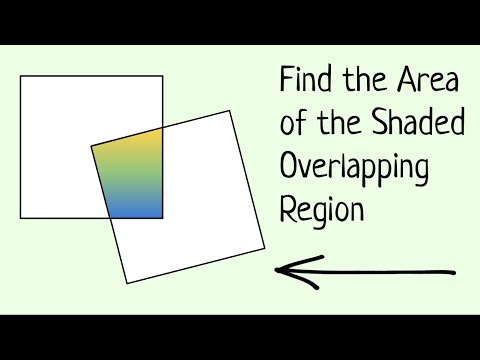
Area of Overlapping Shapes

Spiderweb Math - 0:01:55

Spiderweb Math - Area and Perimeter 1 (Overlapping Squares 1)

AREA OF OVERLAPPING 0:07:54

AREA OF OVERLAPPING CIRCLES

PSLE Math - 0:11:37

PSLE Math - How to solve Overlapping figures and Constant Difference questions!

Finding the Area 0:06:07

Finding the Area of Two Squares OVERLAPPING at one MIDPOINT

Area and Perimeter 0:05:33

Area and Perimeter (Overlapping Rectangles) | Learn Problem Sums | PSLE MATHS PREP

Geometry, Level 3 0:05:58

Geometry, Level 3 of 6, Example 2, Overlapping circles

there are 9 0:07:40

there are 9 square of different colours without overlapping, calculate the area of rectangle ABCD if

31) Find overlapping 0:01:00

31) Find overlapping area. #maths #matholympiad #geometry

overlapping rectangles | 0:02:38

overlapping rectangles | rectangle area | geometry problems | Masterclass Geometry

Комментарии
Автор

Connect E and C, which makes two triangles, both of heights 3/2, and bases 1 and 2.
Area = ½*3/2 *(1+2)=9/4

harikatragadda
Автор

Rotate the right angle FEH by 90°, 180°, 270° respectively. Then you have 4 regions, each with the same area as the shaded area. Together they fill they square ABCD, which has area 3·3 = 9. Hence the area is 9/4.

Bruno_Haible
Автор

Another possibility:
Extend the sides of the big square till they intersect the sides of the small square, thus making four Quadrilaterals. Since these extended lines are orthogonal, they make the same angles at the sides of the small square, and thus the four quadrilaterals are Similar. But the diagonals of the Quadrilaterals are also equal, hence they are also Congruent. Therefore Area of each quadrilateral = ¼(Area of the small square)= 9/4

harikatragadda