filmov
tv
Solving the Quartic x^4-16x-12=0
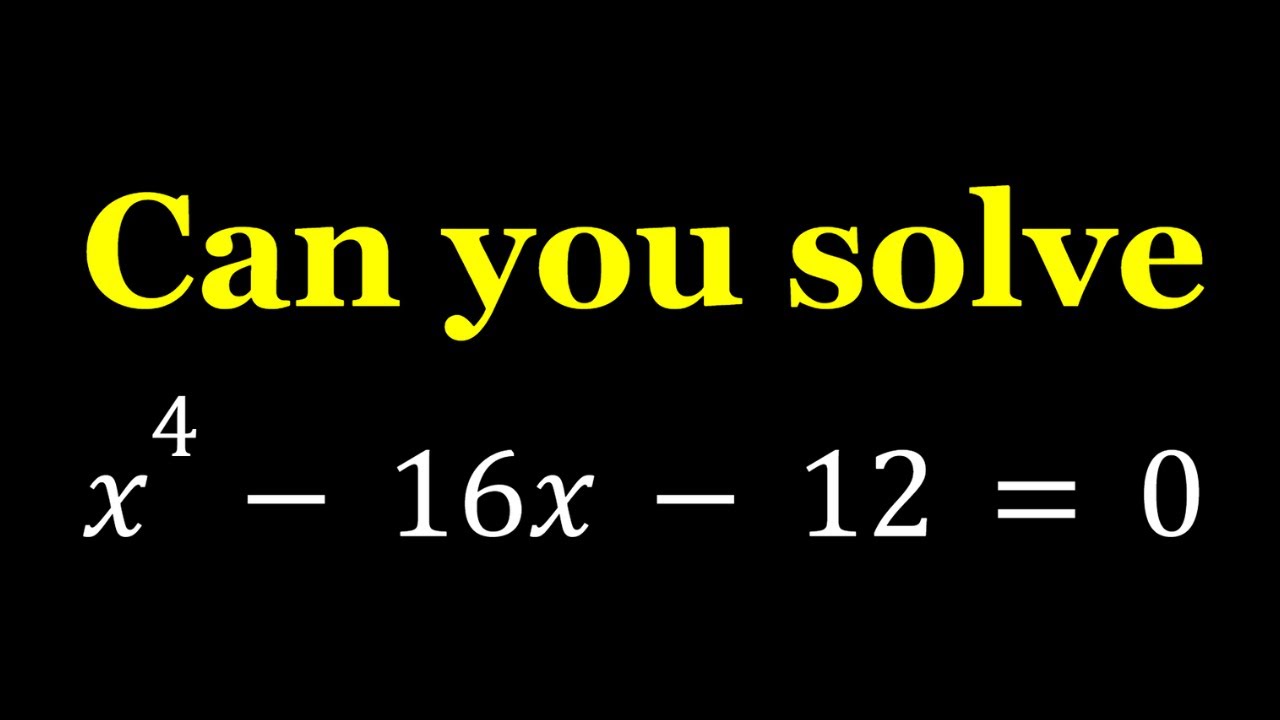
Показать описание
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #PolynomialEquations
SIMILAR PROBLEMS
PLAYLISTS 🎵 :
#ChallengingMathProblems #PolynomialEquations
SIMILAR PROBLEMS
PLAYLISTS 🎵 :
Solving the Quartic x^4-16x-12=0
Beautiful Solution to the Difficult Quartic Equation x^4-16x-12=0 | Math Olympiad
Factoring a polynomial to the fourth power using factoring to second power
x^4+16x-12 |How To Solve Polynomial Quartic Equation#maths #olympiadmathematics#exponentialequation
Solve quadratic equation by factorisation
Solving a quadratic by completing the square
Quadratic Equations | Solve by factoring | Free Math Videos
Solve by completing the square | Step by Step Technique
Math Olympiad • Can You Solve this Mind-Blowing Exponential Equation?
Factor a 4th Degree Polynomial 3x^4 -16x^3 +21x² + 4x-12=0 | Explain in Detailed |
Solve by Completing the Square: Step-by-Step Technique
Quadratic Equation Shortcut Trick | Solve Equation in 5 Seconds
Solve Quadratic Equations By Factoring - Simple Trick No Fuss!
How to find the roots of a polynomials by factoring
Learn how to solve by factoring a quadratic ac method
How to Solve Quadratic Equations by Completing the Square? Grade 9 Math
FERRARI METHOD #2 - MATHEMATICS- HINDI
How to Solve Quadratic Equations Using 3 Methods - Leading Coefficient Other than One
Factor and Solve Cubic Equations in Less Than One Minute! - Super Simple Trick
Solving an equation with variables on both side and one solution
Quadratic Equations (Solve 4x² - 16=0)
Quadratic Equations IIT Questions No 05 ( X Class)
CUBIC EQUATION FACTORIZATION SHORTCUT/ SOLVING CUBIC EQUATIONS IN 10 SECONDS/ Math Tricks.
Partial Fractions - Denominator with quadratic factors | SHS 1 ELECTIVE MATH
Комментарии
 0:10:43
0:10:43
 0:04:21
0:04:21
 0:03:26
0:03:26
 0:04:19
0:04:19
 0:09:05
0:09:05
 0:10:43
0:10:43
 0:02:43
0:02:43
 0:05:20
0:05:20
 0:09:45
0:09:45
 0:39:54
0:39:54
 0:07:40
0:07:40
 0:00:30
0:00:30
 0:06:31
0:06:31
 0:02:43
0:02:43
 0:03:41
0:03:41
 0:06:32
0:06:32
 0:08:02
0:08:02
 0:12:52
0:12:52
 0:07:18
0:07:18
 0:02:36
0:02:36
 0:00:44
0:00:44
 0:00:57
0:00:57
 0:12:06
0:12:06
 0:08:20
0:08:20