filmov
tv
Olympiad Question! Can you solve this? | Brain Teaser!

Показать описание
Norway Math Olympiad Question | You should be able to solve this!
Luxembourg - Math Olympiad Question | You should know this trick
Math Olympiad Question | Equation solving | You should learn this trick to pass the exam
A Nice Olympiad Exponential Multiplication Problem #short #olympiad #mathematics #maths #exponents
A Nice Math Olympiad Exponential Equation 3^x = X^9
France - Math Olympiad Question | An Algebraic Expression | You should be able to solve this!
A beautiful international math olympiad problem
Can you solve this Olympiad question??
Mexico - A Nice Math Olympiad Exponential Problem
Math Olympiad Question | You should know how to solve this!!
Russia | Math Olympiad Question | You should know this trick!!
Math Olympiad Question | Can You Solve This?
The unexpectedly hard windmill question (2011 IMO, Q2)
A math Olympiad exponential math question| Many failed this| Can you solve for x? Exponents.
Math Olympiad 3^m–2^m=65 | Math Olympiad Problems | Algebra
Can you solve this Olympiad question??
UK - Math Olympiad Question | You should be able to solve this without calculators!!
Math Olympiad Question | Nice Algebra Equation | You should know this trick!!
Math Olympiad| can you solve this?| exponential question
Can you solve this Olympiad question??
Can you solve this maths olympiad question?
Can you solve this Olympiad question??
Can you solve this maths olympiad question?
Can you solve this Korean Maths Olympiad Problem 😳 Maths Challenge 📢 #ytshorts #byju #challenge...
Комментарии
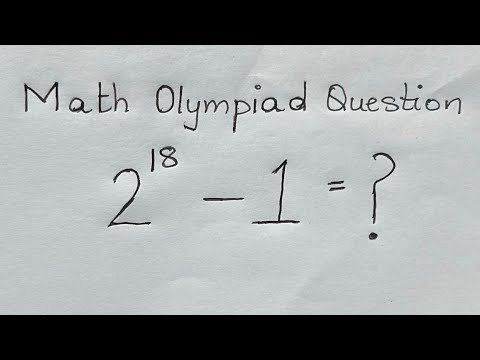 0:03:21
0:03:21
 0:02:51
0:02:51
 0:01:54
0:01:54
 0:00:52
0:00:52
 0:02:34
0:02:34
 0:08:40
0:08:40
 0:01:00
0:01:00
 0:05:09
0:05:09
 0:08:36
0:08:36
 0:02:24
0:02:24
 0:08:01
0:08:01
 0:03:28
0:03:28
 0:16:03
0:16:03
 0:09:52
0:09:52
 0:10:49
0:10:49
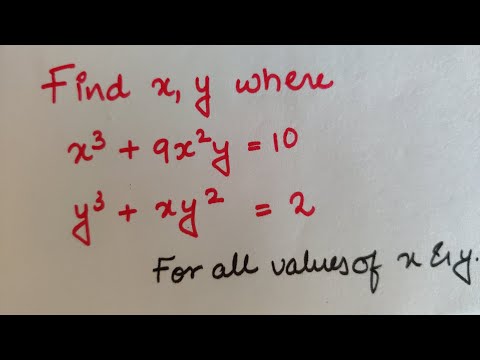 0:10:34
0:10:34
 0:03:20
0:03:20
 0:07:26
0:07:26
 0:12:41
0:12:41
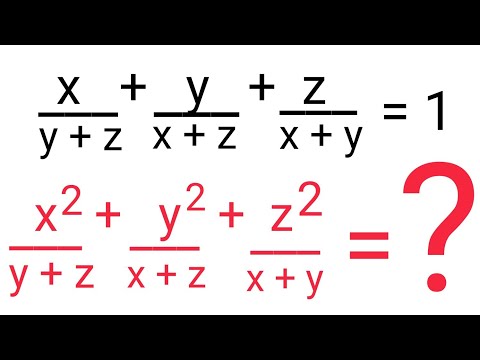 0:08:02
0:08:02
 0:01:58
0:01:58
 0:08:05
0:08:05
 0:01:37
0:01:37
 0:00:50
0:00:50