filmov
tv
1/x+y = 1/x + 1/y
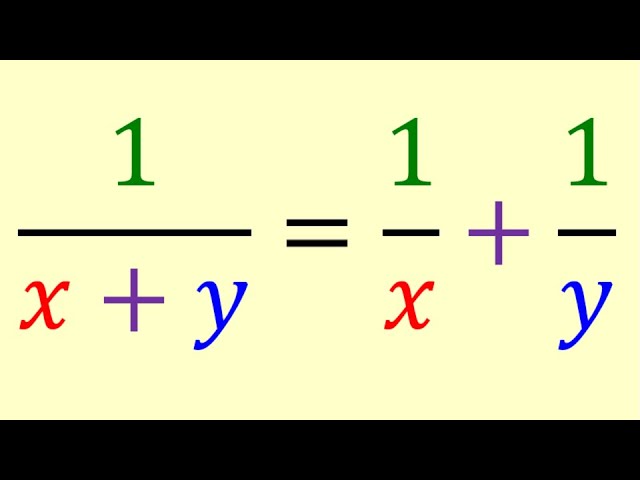
Показать описание
In school you were taught that 1/x+y is not the same as 1/x + 1/y, but for which x and y is it actually true? Watch this video and find out!
1/x+y = 1/x + 1/y
RÉSOUDRE 1/x + 1/y = 1/10
How to Graph the Equation y = 1/x (y equals one over x)
Find the value of x and y
Solving an equation for y and x
5 simple unsolvable equations
How REAL Men Integrate Functions
Simplify a Complex Fraction 1/(1/x+1/y)
Binom Açılımı 1 | Sayma ve Olasılık 10 | 10.SINIF MATEMATİK MatBook | 2025
When mathematicians get bored (ep1)
Find Domain and Range of function y = 1/x
Sistema de Equações do 1º Grau (METÓDO DA ADIÇÃO).
How to Graph y = x + 1
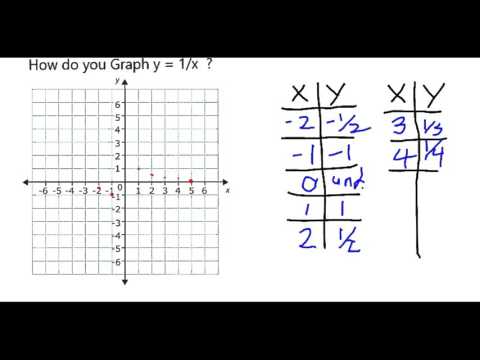
How do you Graph y = 1/x?
y(1+xy)dx+x(1-xy)dy=0 #NonExact L575 @MathsPulseChinnaiahKalpana
Determine whether an equation determines y as a functions of x
Domain of f(x, y) = 1/(xy)
HW # 6 Reflecting over y = -1
📐✏️ Gráfica de la 𝗙𝗨𝗡𝗖𝗜𝗢𝗡 𝗥𝗔𝗖𝗜𝗢𝗡𝗔𝗟 y=1/x | Conoce sus PROPIEDADES...
graficar f(x)=x+1 . y=x+1 . Grafico de funciones lineales , rectas , tabulando
Bernoulli Differential Equation x*dy/dx + y = 1/y^2
Probability Density Function of Z=X+Y : Example 1
Find Domain and Range of function y = 1/(x - 2)
Solving an equation for y and x using two steps
Комментарии
 0:05:13
0:05:13
 0:10:10
0:10:10
 0:02:23
0:02:23
 0:04:55
0:04:55
 0:03:47
0:03:47
 0:00:50
0:00:50
 0:00:35
0:00:35
 0:03:36
0:03:36
 0:34:49
0:34:49
 0:00:37
0:00:37
 0:01:05
0:01:05
 0:07:42
0:07:42
 0:01:19
0:01:19
 0:04:16
0:04:16
 0:22:46
0:22:46
 0:02:53
0:02:53
 0:01:35
0:01:35
 0:01:58
0:01:58
 0:01:58
0:01:58
 0:01:12
0:01:12
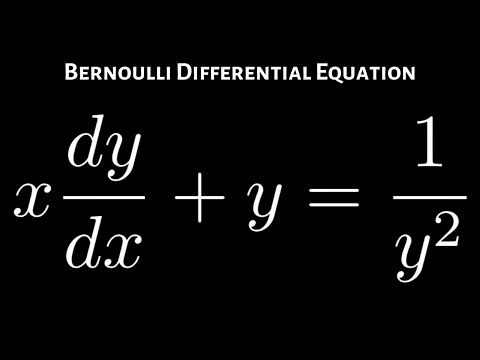 0:11:11
0:11:11
 0:07:58
0:07:58
 0:00:48
0:00:48
 0:03:12
0:03:12