filmov
tv
A Very Nice Algebra Problem | Math Olympiad

Показать описание
A Very Nice Algebra Problem | Math Olympiad
x^2 - x - 1 = 0
(x^16 - 1) /(x^8 + 2x^7) = ?
x^2 - x - 1 = 0
(x^16 - 1) /(x^8 + 2x^7) = ?
A Very Nice Algebra Problem | Fill in the boxes
Math Olympiad | A Very Nice Algebra Problem
A Nice Exponential Algebra Problem | Olympiad Mathematics
China | A Very Nice Algebra Problem | Math Olympiad
Japanese Math Olympiad | A Very Nice Algebra Problem
Can you find the value of this root number | A very nice math question
A very nice algebra problem | You should know this trick #algebra
A Very Nice Math Olympiad Problem | Can You Solve for x? | Algebra
A beautiful ✍️nice exponential maths problem
Thailand | Math Olympiad Question | Nice Algebra Equation
A Very Nice Math Olympiad Problem | Solve for a, b and c | Algebra
Math Olympiad | A Very Nice Geometry Problem | 2 Different Methods
Math Olympiad 3^m–2^m=65 | Math Olympiad Problems | Algebra
Peru | A Nice Algebra Problem | Math Olympiad
Math Olympiad Question | Nice Algebra Equation | You should know this trick!!
Math Olympiad | A Very Nice Geometry Problem | 2 Methods
Brazil | A Nice Algebra Problem | Math Olympiad
Canada | Math Olympiad | A Nice Algebra Problem
The Hardest Math Test
China | Math Olympiad | A Nice Algebra Problem 👇
The unexpectedly hard windmill question (2011 IMO, Q2)
Math Olympiad Problem | A Nice Algebra Challenge
China | A Very Nice Algebra Problem
Linear Algebra Book With Solutions
Комментарии
 0:07:59
0:07:59
 0:08:38
0:08:38
 0:08:50
0:08:50
 0:10:20
0:10:20
 0:07:50
0:07:50
 0:06:10
0:06:10
 0:01:52
0:01:52
 0:16:52
0:16:52
 0:01:51
0:01:51
 0:01:26
0:01:26
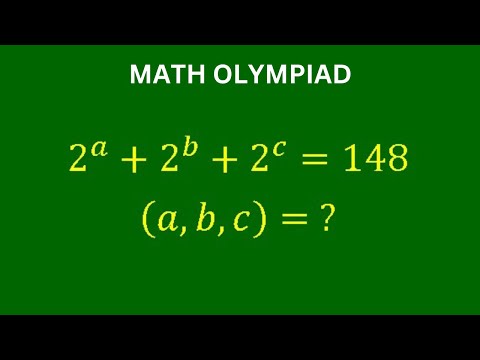 0:12:31
0:12:31
 0:13:04
0:13:04
 0:10:49
0:10:49
 0:13:49
0:13:49
 0:07:26
0:07:26
 0:13:46
0:13:46
 0:18:47
0:18:47
 0:10:20
0:10:20
 0:00:28
0:00:28
 0:10:37
0:10:37
 0:16:03
0:16:03
 0:09:51
0:09:51
 0:07:40
0:07:40
 0:00:46
0:00:46