filmov
tv
A Very Nice Math Olympiad Problem | Solve for a, b and c | Algebra

Показать описание
In this video, I'll be showing you step by step on how to solve this Olympiad Maths Exponential problem using a simple trick.
Please feel free to share your ideas in the comment section.
And if you are new here and you enjoy my content, please hit the like button and subscribe to my channel. Don't forget to hit the bell icon as well so you don't miss on my upcoming videos.
Please feel free to share your ideas in the comment section.
And if you are new here and you enjoy my content, please hit the like button and subscribe to my channel. Don't forget to hit the bell icon as well so you don't miss on my upcoming videos.
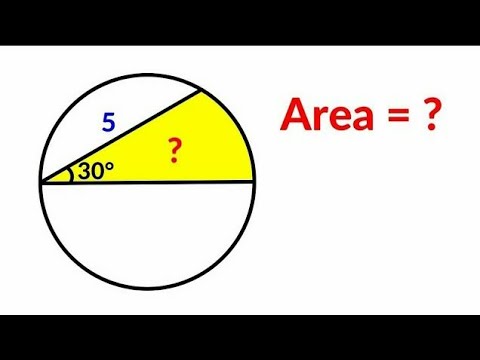
Math Olympiad | A Very Nice Geometry Problem
Olympiad Mathematics | A Very Nice Geometry Problem
A Very Nice Math Olympiad Problem | Solve for x | Algebra
Germany |A Nice Math Olympiad Problem👇
A Very Nice Math Olympiad Problem | Solve for n | Algebra
A Nice Math Olympiad Exponential Equation 3^x = X^9
Math Olympiad | A Very Nice Geometry Problem | 2 Methods
Math Olympiad | A Very Nice Geometry Problem | 2 Different Methods
Japanese | Can You Solve this ? | Math Olympiad😃
Japanese l Very Nice Olympiad Math Tricky Problem l How to solve for x & y ??
A Very Nice Math Olympiad Problem | Solve for a, b and c | Algebra
A Very Nice Math Olympiad Problem | Solve for x | Algebra
A Nice Math Olympiad exponential question| Solve for x
A Very Nice Math Olympiad Problem | Can You Solve for x? | Algebra
A beautiful international math olympiad problem
A Nice Olympiad Exponential Multiplication Problem #short #olympiad #mathematics #maths #exponents
Math Olympiad | A Very Nice Algebra Problem
Mexico - A Nice Math Olympiad Exponential Problem
Thailand | Math Olympiad Question | Nice Algebra Equation
China | Math Olympiad | A Nice Algebra Problem 👇👇👇
Math Olympiad | A Very Nice Geometry Problem
A Very Nice Math Olympiad Problem | Solve for real value of x for which x^30+x^20=80
A Very Nice Math Olympiad Problem | Solve for all solutions of y
Japanese Math Olympiad | A Very Nice Algebra Problem
Комментарии
 0:12:38
0:12:38
 0:11:17
0:11:17
 0:16:04
0:16:04
 0:09:14
0:09:14
 0:07:41
0:07:41
 0:02:34
0:02:34
 0:13:46
0:13:46
 0:13:04
0:13:04
 0:08:04
0:08:04
 0:13:49
0:13:49
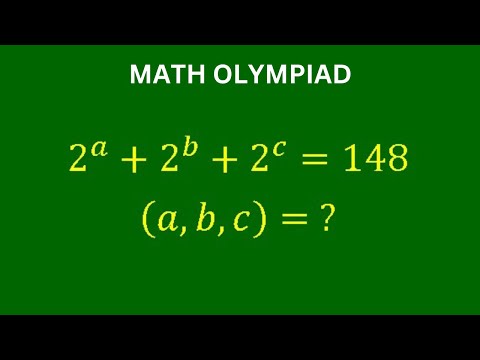 0:12:31
0:12:31
 0:28:12
0:28:12
 0:09:43
0:09:43
 0:16:52
0:16:52
 0:01:00
0:01:00
 0:00:52
0:00:52
 0:08:38
0:08:38
 0:08:36
0:08:36
 0:01:26
0:01:26
 0:13:13
0:13:13
 0:11:45
0:11:45
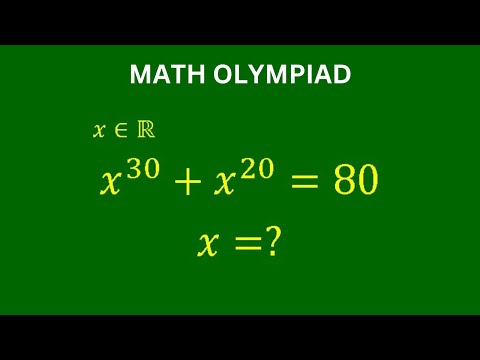 0:10:30
0:10:30
 0:23:42
0:23:42
 0:07:50
0:07:50