Normal force on a tilted surface, parallel and perpendicular weight components + example.

00:00 Summary: We start by deriving the normal force on a tilted surface and the parallel and perpendicular weight components on the inclined plane, then we work an example of a mass on an incline with a string holding it in place then the mass accelerating down the ramp when the string is cut.

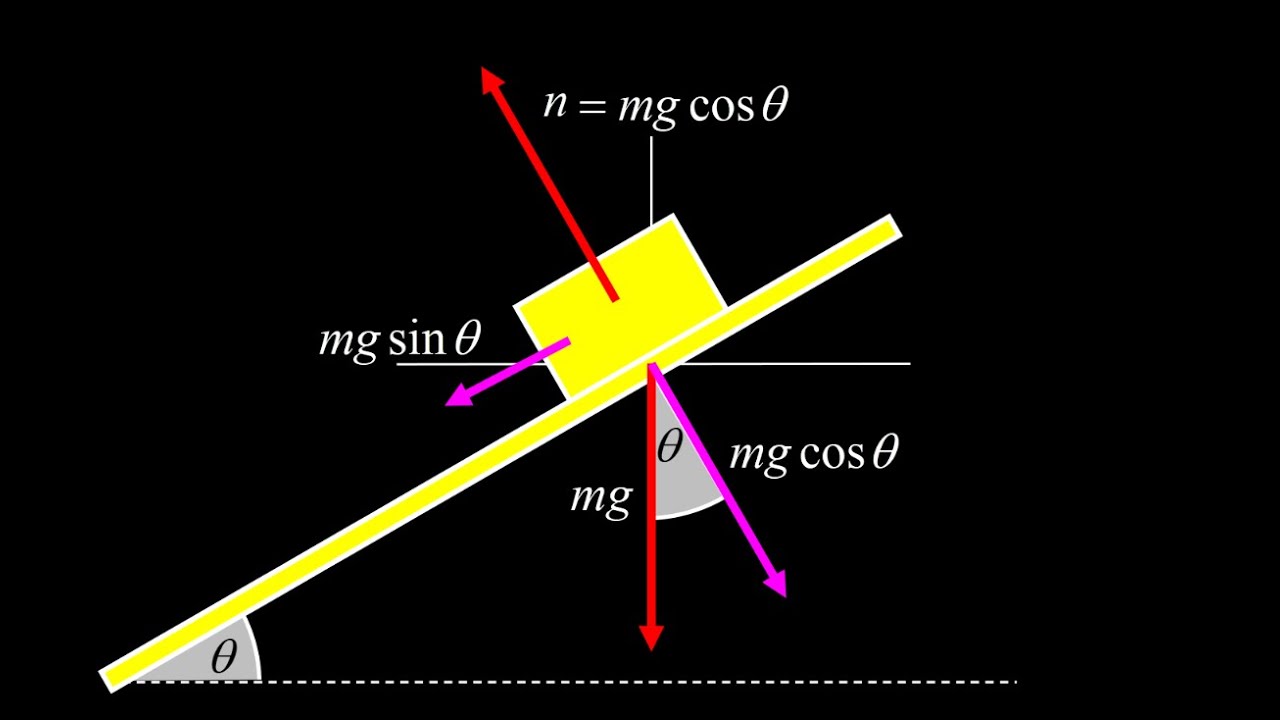
00:10 Setup: normal force and weight components for a mass on a tilted surface. We get the force vectors into the diagram for the mass on the incline: first the force of gravity which points straight down and has a magnitude of mg, then the normal force, which points perpendicular to the ramp and has a magnitude just right to guarantee that the sum of forces perpendicular to the ramp will vanish. This means the acceleration perpendicular to the ramp is zero; in other words, the normal force is what constrains the mass to the surface of the ramp! We introduce the natural coordinates for the inclined plane problem: the coordinate axes are tilted because the normal force is perpendicular to the ramp and the acceleration (if any) is parallel to the ramp. Making the acceleration point down one of the coordinate axes greatly simplifies the problem.

01:06 Components of the weight vector (gravity on a tilted surface): the force of gravity splits into perpendicular and parallel components of mg in our tilted coordinate system, but how do we find the angle required to do the trigonometry here? We need the angle between the vertical and the perpendicular, and we provide a visual proof of the angle. Starting with a level surface, we show an animation of the incline increasing. The angle is traced out simultaneously between the rotating axes and the fixed axes, and between the incline and the horizontal. These angles are exactly the same! Therefore, the angle of incline is the same as the angle between the vertical and perpendicular!

01:59 Finish solving the general problem: now that we have the angle, we can decompose the weight vector into its components: mgsin(theta) perpendicular to the ramp and mgsin(theta) parallel to the ramp. We translate the parallel vector to attach it to the mass. Next, we show the normal force for a mass on an incline. Because the net force perpendicular to the surface must vanish, we conclude that the magnitude of the normal force is mgcos(theta) as well. Now we're ready to apply these ideas to an example!

03:00 Worked example of a mass on an inclined plane: we are given a mass on a tilted surface and given the angle of incline. A string holds the mass in place on the ramp. In the first part of the problem, we get the tension in the string holding the mass up by analyzing the parallel forces on the ramp. In the second part of the problem, we get the normal force for the mass on a ramp by analyzing forces in the perpendicular direction. Finally, we cut the string and allow the mass to accelerate down the ramp. We calculate the acceleration of the mass down the ramp by using Newton's second law one more time (in a coordinate system where down the ramp is positive), and we get the acceleration down the ramp.

[jordiwang]

youtube algorithm is doing bad its job, even though I came to understand another another thing of the concept, your video still was really helpful and allowed me to have a much better understanding of the topic. Amazing job man,

[samiracohen]

I like your in-depth and detailed explanation, but your calculations would be so much easier to follow if you showed units and unit cancellations. For example it would help to know where your final units for acceleration came from.